
定义数列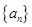 :
: 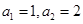 ,且对任意正整数
,且对任意正整数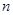 ,有
,有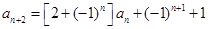 .
.
(1)求数列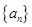 的通项公式与前
的通项公式与前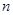 项和
项和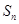 ;
;
(2)问是否存在正整数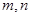 ,使得
,使得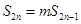 ?若存在,则求出所有的正整数对
?若存在,则求出所有的正整数对
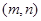 ;若不存在,则加以证明.
;若不存在,则加以证明.
(1)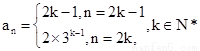 ,
,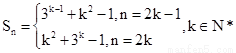 ;
;
(2)见解析.
【解析】考查了等差、等比数列的通项公式、求和公式,数列的分组求和等知识,考查了学生变形的能力,推理能力,探究问题的能力,分类讨论的数学思想、化归与转化的思想以及创新意识.
解:(1)对任意正整数k,
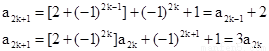 ,
,
. 1分
所以数列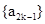 是首项
是首项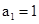 ,公差为2等差数列;数列
,公差为2等差数列;数列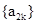 是首项
是首项
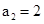 ,公比为3的等比数列. 2分
,公比为3的等比数列. 2分
对任意正整数k, 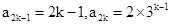 ,. 3分
,. 3分
所以数列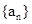 的通项公式
的通项公式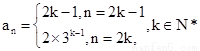 4分
4分
对任意正整数k,
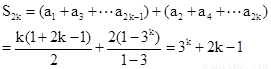 . 5分
. 5分
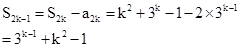 6分
6分
所以数列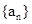 的前n项和为
的前n项和为
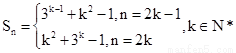 . 7分
. 7分
(2) 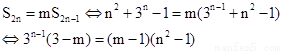 ,
,
从而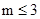 ,由
,由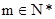 知m=1,2,3 8分
知m=1,2,3 8分
①当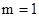 时,
时,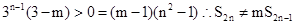 9分
9分
②当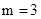 时,
时, 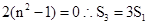 10分
10分
③当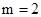 时,
时,
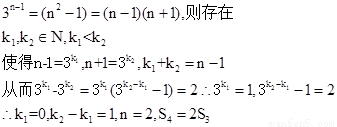 13分
13分
综上可知,符合条件的正整数对(m,n)只有两对:(2,2,)与(3,1) 14分


科目:高中数学 来源: 题型:
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
| an+an+2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
|
|
|
|
|
|
| 1 |
| an |
| an+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省、临川一中高三12月联考文科数学试卷(解析版) 题型:选择题
已知函数 ,若数列
,若数列 满足
满足 ,且对任意正整数
,且对任意正整数 都有
都有 成立,则实数
成立,则实数 的取值范围是( )
的取值范围是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com