
【题目】已知f(x)=xlnx,g(x)= ![]() ,直线l:y=(k﹣3)x﹣k+2
,直线l:y=(k﹣3)x﹣k+2
(1)函数f(x)在x=e处的切线与直线l平行,求实数k的值
(2)若至少存在一个x0∈[1,e]使f(x0)<g(x0)成立,求实数a的取值范围
(3)设k∈Z,当x>1时f(x)的图象恒在直线l的上方,求k的最大值.
【答案】
(1)解:∵f′(x)=1+lnx,
∴f′(e)=1+lne=k﹣3
∴k=5,
(2)解:由于存在x0∈[1,e],使f(x0)<g(x0),
则 ![]() ax02>x0lnx0,
ax02>x0lnx0,
∴a> ![]()
设h(x)= ![]()
则h′(x)= ![]() ,
,
当x∈[1,e]时,h′(x)≥0(仅当x=e时取等号)
∴h(x)在[1,e]上单调递增,
∴h(x)min=h(1)=0,因此a>0
(3)解:由题意xlnx>(k﹣3)x﹣k+2在x>1时恒成立
即k< ![]() ,
,
设F(x)= ![]() ,
,
∴F′(x)= ![]() ,
,
令m(x)=x﹣lnx﹣2,则m′(x)=1﹣ ![]() =
= ![]() >0在x>1时恒成立
>0在x>1时恒成立
所以m(x)在(1,+∞)上单调递增,且m(3)=1﹣ln3<0,m(4)=2﹣ln4>0,
所以在(1,+∞)上存在唯一实数x0(x0∈(3,4))使m(x)=0
当1<x<x0时m(x)<0即F′(x)<0,
当x><x0时m(x)>0即F′(x)>0,
所以F(x)在(1,x0)上单调递减,在(x0,+∞)上单调递增,
F(x)min=F(x0)= ![]() =
= ![]() =x0+2∈(5,6)
=x0+2∈(5,6)
故k<x0+2又k∈Z,所以k的最大值为5
【解析】(1)先求导,根据导数的几何意义得到关于k的方程解得即可.(2)由于存在x0∈[1,e],使f(x0)<g(x0),则kx0>2lnx0a> ![]() ,只需要k大于h(x)=
,只需要k大于h(x)= ![]() 的最小值即可.(3)分离参数,得到k<
的最小值即可.(3)分离参数,得到k< ![]() ,构造函数,求函数的最小值即可.
,构造函数,求函数的最小值即可.
【考点精析】关于本题考查的函数的最大(小)值与导数,需要了解求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能得出正确答案.
比较,其中最大的是一个最大值,最小的是最小值才能得出正确答案.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为 ![]() (θ为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρcosθ=﹣2.
(θ为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρcosθ=﹣2.
(1)求C1和C2在直角坐标系下的普通方程;
(2)已知直线l:y=x和曲线C1交于M,N两点,求弦MN中点的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn=2n2+n,n∈N* .
(1)求{an}的通项公式;
(2)若数列{bn}满足an=4log2bn+3,n∈N* , 求数列{anbn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知⊙O是△ABC的外接圆,AB=BC,AD是BC边上的高,AE是⊙O的直径. 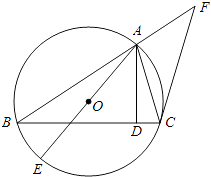
(1)求证:ACBC=ADAE;
(2)过点C作⊙O的切线交BA的延长线于点F,若AF=4,CF=6,求AC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市举办校园足球赛,组委会为了做好服务工作,招募了12名男志愿者和10名女志愿者,调查发现男女志愿者中分别有8人和4人喜欢看足球比赛,其余不喜欢
(1)根据以上数据完成以下2×2列联表:
喜欢看足球比赛 | 不喜欢看足球比赛 | 总计 | |
男 | |||
女 | |||
总计 |
(2)根据列联表的独立性检验,能否在犯错误的概率不超过0.10的前提下认为性别与喜欢看足球比赛有关?
(3)从女志愿者中抽取2人参加某场足球比赛服务工作,若其中喜欢看足球比赛的人数为ξ,求ξ的分布列和数学期望.
附:参考公式:K2= ![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
参考数据:
P(K2≥k0) | 0.4 | 0.25 | 0.10 | 0.010 |
k0 | 0.708 | 1.323 | 2.706 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A、B、C所对的边长分别为a,b,c且满足csinA= ![]() acosC,则sinA+sinB的最大值是( )
acosC,则sinA+sinB的最大值是( )
A.1
B.![]()
C.3
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={(x,y)|(x﹣4)2+y2=1},B={(x,y)|(x﹣t)2+(y﹣at+2)2=1},如果命题“t∈R,A∩B≠”是真命题,则实数a的取值范围是( )
A.[1,4]
B.[0, ![]() ]
]
C.[0, ![]() ]
]
D.(﹣∞,0]∪( ![]() ,+∞]
,+∞]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解一个英语教改实验班的情况,举行了一次测试,将该班30位学生的英语成绩进行统计,得图示频率分布直方图,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100]. 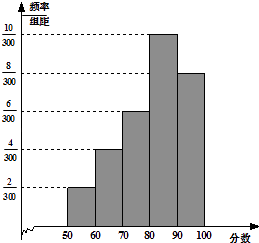
(1)求出该班学生英语成绩的众数,平均数及中位数;
(2)从成绩低于80分的学生中随机抽取2人,规定抽到的学生成绩在[50,60)的记1绩点分,在[60,80)的记2绩点分,设抽取2人的总绩点分为ξ,求ξ的分布列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com