
分析 (1)判断出$\overrightarrow{a}$与$\overrightarrow{b}$不能平行,利用向量平行的坐标运算列出方程,由二倍角的余弦公式化简后,由余弦函数的值域进行判断;
(2)由向量的数量积坐标运算、二倍角的余弦公式以及变形化简f(x),由正弦函数的性质和f(x)的单调性求出f(x)的最小值.
解答 解:(1)$\overrightarrow{a}$与$\overrightarrow{b}$不能平行,原因如下:
若向量$\overrightarrow{a}$=($\frac{1}{sinx}$,$\frac{-1}{sinx}$),$\overrightarrow{b}$=(2,cos2x-sin2x)平行,
则$\frac{1}{sinx}×(co{s}^{2}x-si{n}^{2}x)-(\frac{-1}{sinx}×2)$=0,
$\frac{1}{sinx}(cos2x+2)=0$,
∵$\frac{1}{sinx}≠0$,∴cos2x+2=0,即cos2x=-2不成立,
∴$\overrightarrow{a}$与$\overrightarrow{b}$不能平行;
(2)f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{2}{sinx}-\frac{1}{sinx}(co{s}^{2}x-si{n}^{2}x)$
=$\frac{1}{sinx}•(2-cos2x)$=$\frac{1}{sinx}•(3-2si{n}^{2}x)$
=$\frac{3}{sinx}-2sinx$,
由x∈(0,$\frac{π}{3}$]得,sinx∈(0,$\frac{\sqrt{3}}{2}$],
∵f(x)=$\frac{3}{sinx}-2sinx$随着sinx的增大而减小,
∴当sinx=$\frac{\sqrt{3}}{2}$时,f(x)取到最小值是$\sqrt{3}$.
点评 本题考查正弦函数的性质,向量平行、向量数量积的坐标运算,二倍角余弦公式以及变形,考查化简、变形能力.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:选择题
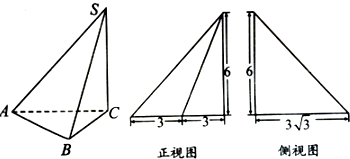
| A. | 84π | B. | 72π | C. | 60π | D. | 48π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 20π-8+4$\sqrt{14}$ | B. | 20π+2$\sqrt{14}$ | C. | 20π-8+2$\sqrt{14}$ | D. | 20π+4$\sqrt{14}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 20072 | D. | 2007 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知一个几何体的三视图如图所示,其中正视图和俯视图是全等的等腰直角三角形,则这个几何体外接球体积与该几何体的体积之比为( )
已知一个几何体的三视图如图所示,其中正视图和俯视图是全等的等腰直角三角形,则这个几何体外接球体积与该几何体的体积之比为( )| A. | $\frac{3\sqrt{3}}{2}$π | B. | $\frac{\sqrt{3}}{4}$π | C. | $\frac{3\sqrt{3}}{4}$π | D. | $\frac{\sqrt{3}}{8}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
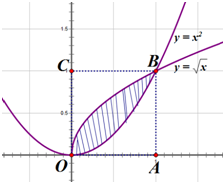 如图,设区域D={(x,y)|0≤x≤1,0≤y≤1,向区域内随机投一点,且投入到区域内任一点都是等可能的,则点落到由曲线y=$\sqrt{x}$与y=x2所围成阴影区域内的概率是( )
如图,设区域D={(x,y)|0≤x≤1,0≤y≤1,向区域内随机投一点,且投入到区域内任一点都是等可能的,则点落到由曲线y=$\sqrt{x}$与y=x2所围成阴影区域内的概率是( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com