
【题目】如图,![]() ,
,![]() 是通过某城市开发区中心O的两条南北和东西走向的街道,链接M,N两地之间的铁路是圆心在
是通过某城市开发区中心O的两条南北和东西走向的街道,链接M,N两地之间的铁路是圆心在![]() 上的一段圆弧,若点M在O正北方向,且
上的一段圆弧,若点M在O正北方向,且![]() ,点N到
,点N到![]() ,
,![]() 距离分别为4km和5km.
距离分别为4km和5km.
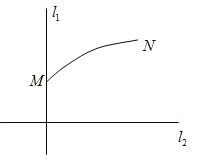
![]() 建立适当的坐标系,求铁路线所在圆弧的方程;
建立适当的坐标系,求铁路线所在圆弧的方程;
![]() 若该城市的某中学拟在O点正东方向选址建分校,考虑环境问题,要求校址到点O的距离大于4km,并且铁路线上任意一点到校址的距离不能少于
若该城市的某中学拟在O点正东方向选址建分校,考虑环境问题,要求校址到点O的距离大于4km,并且铁路线上任意一点到校址的距离不能少于![]() ,求该校址距离点O的最近距离.
,求该校址距离点O的最近距离.![]() 注:校址视为一个点
注:校址视为一个点![]()
科目:高中数学 来源: 题型:
【题目】图1是由矩形![]() 和菱形
和菱形![]() 组成的一个平面图形,其中
组成的一个平面图形,其中![]() ,
, ![]() ,将其沿
,将其沿![]() 折起使得
折起使得![]() 与
与![]() 重合,连结
重合,连结![]() ,如图2.
,如图2.
(1)证明图2中的![]() 四点共面,且平面
四点共面,且平面![]() 平面
平面![]() ;
;
(2)求图2中的四边形![]() 的面积.
的面积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() ,圆
,圆![]() 与圆
与圆![]() 关于直线
关于直线![]() :
:![]() 对称.
对称.
(1)求圆![]() 的方程;
的方程;
(2)过直线![]() 上的点
上的点![]() 分别作斜率为
分别作斜率为![]() ,4的两条直线
,4的两条直线![]() ,
,![]() ,使得
,使得![]() 被圆
被圆![]() 截得的弦长与
截得的弦长与![]() 被圆
被圆![]() 截得的弦长相等.
截得的弦长相等.
(i)求点![]() 的坐标;
的坐标;
(ii)过点![]() 任作两条互相垂直的直线分别与两圆相交,判断所得弦长是否恒相等,并说明理由.
任作两条互相垂直的直线分别与两圆相交,判断所得弦长是否恒相等,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某赛季,甲、乙两名篮球运动员都参加了![]() 场比赛,他们所有比赛得分的情况如下:
场比赛,他们所有比赛得分的情况如下:
甲:![]() ;
;
乙:![]() .
.
(1)求甲、乙两名运动员得分的中位数.
(2)分别求甲、乙两名运动员得分的平均数、方差,你认为哪位运动员的成绩更稳定?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() :
:![]() (
(![]() ,
,![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() :
:![]() .
.
(1)说明![]() 是哪一种曲线,并将
是哪一种曲线,并将![]() 的方程化为极坐标方程;
的方程化为极坐标方程;
(2)若直线![]() 的方程为
的方程为![]() ,设
,设![]() 与
与![]() 的交点为
的交点为![]() ,
,![]() ,
,![]() 与
与![]() 的交点为
的交点为![]() ,
,![]() ,若
,若![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com