

| 甲班(A方式) | 乙班(B方式) | 总计 | |
| 成绩优秀 | |||
| 成绩不优秀 | |||
| 总计 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P≥(k2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2.706 | 3.814 | 5.024 |
| 频数 |
| 总数 |
| ||
|
| 207 |
| 245 |
| ||||
|
| 184 |
| 1225 |
| ||
|
| 6 |
| 1225 |
| 100×(12×46-4×38)2 |
| 16×84×50×50 |
| 频数 |
| 总数 |


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
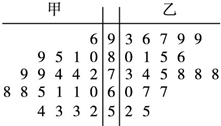 某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A、B两种不同的教学方式分别在甲、乙两个班级进行教改实验.为了解教学效果,期末考试后,陈老师分别从两个班级中各随机抽取20名学生的成绩进行统计,作出茎叶图如下.记成绩不低于90分者为“成绩优秀”.
某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A、B两种不同的教学方式分别在甲、乙两个班级进行教改实验.为了解教学效果,期末考试后,陈老师分别从两个班级中各随机抽取20名学生的成绩进行统计,作出茎叶图如下.记成绩不低于90分者为“成绩优秀”.| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| n(n11 n22-n12n21)2 |
| n1+ n2+n+1n+2 |
| P(k2≥K) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源:2014届福建高二下第一次月考理科数学试卷(解析版) 题型:解答题
某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A、B两种不同的教学方式分别在甲、乙两个班级进行教改实验.为了解教学效果,期末考试后,陈老师分别从两个班级中各随机抽取20名学生的成绩进行统计,作出茎叶图如下.记成绩不低于90分者为“成绩优秀”.

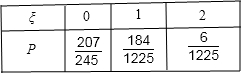
(1)在乙班样本的20个个体中,从不低于86分的成绩中随机抽取2个,求抽出的2个至多一个“成绩优秀”的概率;
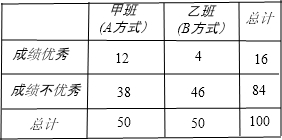
(2)由以上统计数据填写下面列联表,并判断是否有90%的把握认为:“成绩优秀”与教学方式有关.
|
|
甲班 (A方式) |
乙班 (B方式) |
总计 |
|
成绩优秀 |
|
|
|
|
成绩不优秀 |
|
|
|
|
总计 |
|
|
|
附: 
|
|
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
|
k |
1.323 |
2.072 |
2. 706 |
3. 841 |
5. 024 |
查看答案和解析>>
科目:高中数学 来源:2013届河北省高二下学期第四次月考理科数学试卷(解析版) 题型:解答题
(本小题满分12分)某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人.,陈老师采用两种不同的教学方式分别在甲、乙两个班级进行教改实验.为了解教学效果,期末考试后,陈老师对甲、乙两个班级的学生成绩进行统计分析,画出频率直方图(如下图).记成绩不低于90分者为“成绩优秀”.

(I)从乙班随机抽取2名学生的成绩,记“成绩优秀”的人数为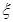 ,求
,求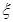 的分布列和数学期望;
的分布列和数学期望;
(II)根据频率分布直方图填写下面 列联表,并判断是否有
列联表,并判断是否有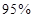 的把握认为:“成绩优秀”与教学方式有关.
的把握认为:“成绩优秀”与教学方式有关.

查看答案和解析>>
科目:高中数学 来源:2011-2012学年河南省豫北六校高三第二次精英联赛考试理科数学试卷 题型:解答题
某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A、B两种不同的教学方式分别在甲、乙两个班级进行教改实验.为了解教学效果,期末考试后,陈老师对甲、乙两个班级的学生成绩进行统计分析,画出频率分布直方图(如右图).记成绩不低于90分者为“成绩优秀”.

(I)从乙班随机抽取2名学生的成绩,记“成绩优秀”的个数为 ,求
,求 的分布列和数学期望;
的分布列和数学期望;
(II)根据频率分布直方图填写下面 列联表,并判断是否有95%的把握认为“成绩优秀”与教学方式有关。
列联表,并判断是否有95%的把握认为“成绩优秀”与教学方式有关。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com