
【题目】某市为了宣传环保知识,举办了一次“环保知识知多少”的问卷调查活动(一人答一份).现从回收的年龄在2060岁的问卷中随机抽取了100份, 统计结果如下面的图表所示.
年龄 分组 | 抽取份 数 | 答对全卷的人数 | 答对全卷的人数占本组的概率 |
[20,30) | 40 | 28 | 0.7 |
[30,40) | n | 27 | 0.9 |
[40,50) | 10 | 4 | b |
[50,60] | 20 | a | 0.1 |

(1)分别求出n, a, b, c的值;
(2)从年龄在[40,60]答对全卷的人中随机抽取2人授予“环保之星”,求年龄在[50,60] 的人中至少有1人被授予“环保之星”的概率.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)根据频率直方分布图,通过概率的和为1,求求出n,a,b,c的值,
(2)年龄在[40,50)中答对全卷的4人记为A,B,C,D,年龄在[50,60]中答对全卷的2人记为a,b,分别列举出所有的基本事件,根据概率公式计算即可.
试题解析:
(1)因为抽取总问卷为100份,所以n=100-(40+10+20)=30.
年龄在![]() 中,抽取份数为10份,答对全卷人数为4人,所以b=
中,抽取份数为10份,答对全卷人数为4人,所以b=![]() =0.4.
=0.4.
年龄在![]() 中,抽取份数为20份,答对全卷人数占本组的概率为0.1,所以
中,抽取份数为20份,答对全卷人数占本组的概率为0.1,所以![]() =0.1,得
=0.1,得![]() .
.
根据频率直方分布图,得(0.04+0.03+c+0.01)×10=1,解得![]() .
.
(2)因为年龄在![]() 与
与![]() 中答对全卷的人数分别为4人与2人.
中答对全卷的人数分别为4人与2人.
年龄在![]() 中答对全卷的4人记为
中答对全卷的4人记为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,年龄在
,年龄在![]() 中答对全卷的2人记为
中答对全卷的2人记为![]() ,
, ![]() ,则从这6人中随机抽取2人授予“环保之星”奖的所有可能的情况是:
,则从这6人中随机抽取2人授予“环保之星”奖的所有可能的情况是: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,共15种(8分).
,共15种(8分).
其中所抽取年龄在![]() 的人中至少有1人被授予“环保之星”的情况是:
的人中至少有1人被授予“环保之星”的情况是: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 共9种.
共9种.
故所求的概率为![]() .
.


科目:高中数学 来源: 题型:
【题目】下列命题中,正确的命题有__________.
①回归直线![]() 恒过样本点的中心
恒过样本点的中心![]() ,且至少过一个样本点;
,且至少过一个样本点;
②将一组数据的每个数据都加一个相同的常数后,方差不变;
③用相关指数![]() 来刻面回归效果;表示预报变量对解释变量变化的贡献率,越接近于1,说明模型的拟合效果越好;
来刻面回归效果;表示预报变量对解释变量变化的贡献率,越接近于1,说明模型的拟合效果越好;
④若分类变量![]() 和
和![]() 的随机变量
的随机变量![]() 的观测值
的观测值![]() 越大,则“
越大,则“![]() 与
与![]() 相关”的可信程度越小;
相关”的可信程度越小;
⑤.对于自变量![]() 和因变量
和因变量![]() ,当
,当![]() 取值一定时,
取值一定时, ![]() 的取值具有一定的随机性,
的取值具有一定的随机性, ![]() ,
, ![]() 间的这种非确定关系叫做函数关系;
间的这种非确定关系叫做函数关系;
⑥.残差图中残差点比较均匀的地落在水平的带状区域中,说明选用的模型比较合适;
⑦.两个模型中残差平方和越小的模型拟合的效果越好.
查看答案和解析>>
科目:高中数学 来源: 题型:
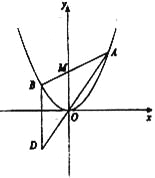
【题目】如图所示,已知抛物线![]() ,过点
,过点![]() 任作一直线与
任作一直线与![]() 相交于
相交于![]() 两点,过点
两点,过点![]() 作
作![]() 轴的平行线与直线
轴的平行线与直线![]() 相交于点
相交于点![]() 为坐标原点).
为坐标原点).
(1)证明: 动点![]() 在定直线上;
在定直线上;
(2)作![]() 的任意一条切线
的任意一条切线![]() (不含
(不含![]() 轴), 与直线
轴), 与直线![]() 相交于点
相交于点![]() 与(1)中的定直线相交于点
与(1)中的定直线相交于点![]() .
.
证明: ![]() 为定值, 并求此定值.
为定值, 并求此定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
: ![]() (
(![]() )的焦点为
)的焦点为![]() ,点
,点![]() 在抛物线
在抛物线![]() 上,且
上,且![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
, ![]() 两点,
两点, ![]() 为坐标原点.
为坐标原点.
(1)求抛物线![]() 的方程;
的方程;
(2)求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}中,a1=2, ![]() (n∈N*).
(n∈N*).
(1)证明数列 ![]() 是等比数列,并求数列{an}的通项公式;
是等比数列,并求数列{an}的通项公式;
(2)设 ![]() ,若数列{bn}的前n项和是Tn , 求证:
,若数列{bn}的前n项和是Tn , 求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线G:x2=2py(p>0),直线y=k(x﹣1)+2与抛物线G相交A(x1 , y1),B(x2 , y2)(x1<x2),过A,B点分别作抛物线G的切线L1 , L2 , 两切线L1 , L2相交H(x,y),
(1)若k=1,有 L1⊥L2 , 求抛物线G的方程;
(2)若p=2,△ABH的面积为S1 , 直线AB与抛物线G围成封闭图形的面积为S2 , 证明: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学从参加环保知识竟赛的学生中抽取了部分学生的成绩进行分析,不过作好的茎叶图和频率分布直方图因故均受到不同程度的损坏,其可见部分信息如图所示,据此解答下列问题:

(1)求抽取学生成绩的中位数,并修复频率分布直方图;
(2)根据修复的频率分布直方图估计该中学此次环保知识竞赛的平均成绩。(以各组的区间中点值代表该组的各个值)
查看答案和解析>>
科目:高中数学 来源: 题型:
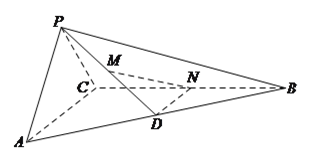
【题目】在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 为
为![]() 的中点,
的中点, ![]() 在棱
在棱![]() 上.
上.
(![]() )当
)当![]() 为
为![]() 的中点时,证明:
的中点时,证明: ![]() 平面
平面![]() .
.
(![]() )求证:
)求证: ![]() 平面
平面![]() .
.
(![]() )是否存在点
)是否存在点![]() 使得
使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com