
【题目】如图:边长为![]() 的菱形
的菱形![]() ,
,![]() ,将
,将![]() 沿
沿![]() 折起到图中
折起到图中![]() 的位置,使得二面角
的位置,使得二面角![]() 的大小为
的大小为![]() ,则三棱锥
,则三棱锥![]() 的外接球表面积等于_______.
的外接球表面积等于_______.

【答案】![]() .
.
【解析】
由题意取BD中点M,则∠DAB=60°为二面角P﹣BD﹣C的平面角,△PMC是边长为3的正三角形,E,F分别为PM,CM靠近M的三等分点,作EO⊥面PBD,FO⊥面BCD,则O为外接球球心.利用球心到各顶点距离相等构造直角三角形求解外接球的半径R,可得答案.
由题意,如图:取BD中点M,
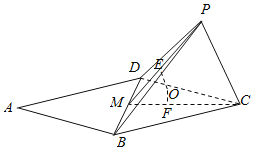
则∠DAB=60°为二面角P﹣BD﹣C的平面角,
△PMC是边长为3的正三角形,E,F分别为PM,CM靠近M的三等分点,
作EO⊥面PBD,FO⊥面BCD,则O为外接球球心.
∵MF=1,PMC=60°,连接OC,OM,可得∠OMC=30°,
∴OF=![]() MO
MO
∴OF=![]()
∵FC=2
∴R2=OF2+FC2=![]()
三棱锥P﹣BCD的外接球表面积S=4πR2=![]()
故答案为:![]() .
.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】下列命题中正确命题的个数是
(1)对分类变量![]() 与
与![]() 的随机变量
的随机变量![]() 的观测值
的观测值![]() 来说,
来说,![]() 越小,判断“
越小,判断“![]() 与
与![]() 有关系”的把握越大;
有关系”的把握越大;
(2)若将一组样本数据中的每个数据都加上同一个常数后,则样本的方差不变;
(3)在残差图,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高;
(4)设随机变量![]() 服从正态分布
服从正态分布![]() ;
;
若![]() ,则
,则![]() ( )
( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年2月9-25日,第23届冬奥会在韩国平昌举行.4年后,第24届冬奥会将在中国北京和张家口举行.为了宣传冬奥会,某大学在平昌冬奥会开幕后的第二天,从全校学生中随机抽取了120名学生,对是否收看平昌冬奥会开幕式情况进行了问卷调查,统计数据如下:
收看 | 没收看 | |
男生 | 60 | 20 |
女生 | 20 | 20 |
(Ⅰ)根据上表说明,能否有![]() 的把握认为,收看开幕式与性别有关?
的把握认为,收看开幕式与性别有关?
(Ⅱ)现从参与问卷调查且收看了开幕式的学生中,采用按性别分层抽样的方法选取8人,参加2022年北京冬奥会志愿者宣传活动.
(ⅰ)问男、女学生各选取多少人?
(ⅱ)若从这8人中随机选取2人到校广播站开展冬奥会及冰雪项目宣传介绍,求恰好选到一名男生一名女生的概率P.
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,点
,点![]() 也为抛物线
也为抛物线![]() 的焦点.(1)若
的焦点.(1)若![]() 为椭圆
为椭圆![]() 上两点,且线段
上两点,且线段![]() 的中点为
的中点为![]() ,求直线
,求直线![]() 的斜率;
的斜率;
(2)若过椭圆![]() 的右焦点
的右焦点![]() 作两条互相垂直的直线分别交椭圆于
作两条互相垂直的直线分别交椭圆于![]() 和
和![]() ,设线段
,设线段![]() 的长分别为
的长分别为![]() ,证明
,证明![]() 是定值.
是定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的导函数为
的导函数为![]() ,且对任意的实数
,且对任意的实数![]() 都有
都有![]() (
(![]() 是自然对数的底数),且
是自然对数的底数),且![]() ,若关于
,若关于![]() 的不等式
的不等式![]() 的解集中恰有两个整数,则实数
的解集中恰有两个整数,则实数![]() 的取值范围是
的取值范围是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】医药公司针对某种疾病开发了一种新型药物,患者单次服用制定规格的该药物后,其体内的药物浓度![]() 随时间
随时间![]() 的变化情况(如图所示):当
的变化情况(如图所示):当![]() 时,
时,![]() 与
与![]() 的函数关系式为
的函数关系式为![]() (
(![]() 为常数);当
为常数);当![]() 时,
时,![]() 与
与![]() 的函数关系式为
的函数关系式为![]() (
(![]() 为常数).服药
为常数).服药![]() 后,患者体内的药物浓度为
后,患者体内的药物浓度为![]() ,这种药物在患者体内的药物浓度不低于最低有效浓度,才有疗效;而超过最低中毒浓度,患者就会有危险.
,这种药物在患者体内的药物浓度不低于最低有效浓度,才有疗效;而超过最低中毒浓度,患者就会有危险.
(1)首次服药后,药物有疗效的时间是多长?
(2)首次服药1小时后,可否立即再次服用同种规格的这种药物?
(参考数据:![]() ,
,![]() )
)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将圆![]() 上每一点的横坐标变为原来的2倍,纵坐标变为原来的4倍,得曲线
上每一点的横坐标变为原来的2倍,纵坐标变为原来的4倍,得曲线![]() .
.
(1)写出![]() 的参数方程;
的参数方程;
(2)设直线![]() 与
与![]() 的交点为
的交点为![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,求过线段
轴正半轴为极轴建立极坐标系,求过线段![]() 的中点与
的中点与![]() 垂直的直线的极坐标方程.
垂直的直线的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=|lnx|,若函数g(x)=f(x)-ax在区间(0,4)上有三个零点,则实数a的取值范围是( )
A. (0,![]() )B. (
)B. (![]() ,e)C. (
,e)C. (![]() ,
,![]() )D. (0,
)D. (0,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com