
【题目】已知 ![]() =(sinx,cosx),
=(sinx,cosx), ![]() =(sinx,k),
=(sinx,k), ![]() =(﹣2cosx,sinx﹣k).
=(﹣2cosx,sinx﹣k).
(1)当x∈[0, ![]() ]时,求|
]时,求| ![]() +
+ ![]() |的取值范围;
|的取值范围;
(2)若g(x)=( ![]() +
+ ![]() )
) ![]() ,求当k为何值时,g(x)的最小值为﹣
,求当k为何值时,g(x)的最小值为﹣ ![]() .
.
【答案】
(1)解: ![]() =(sinx﹣2cosx,sinx),
=(sinx﹣2cosx,sinx),
| ![]() |2=(sinx﹣2cosx,sinx)2
|2=(sinx﹣2cosx,sinx)2
=2sin2x﹣4sinxcosx+4cos2x
=2cos2x﹣4sinxcosx+2
=cos2x﹣2sin2x+3
= ![]() cos(2x+φ)+3,其中,tanφ=2,
cos(2x+φ)+3,其中,tanφ=2,
又∵x∈[0, ![]() ],
],
∴ ![]() ,
,
∴ ![]() 在
在 ![]() 上单调递减,
上单调递减,
∴| ![]() cos(2x+φ)|2∈[1,4],
cos(2x+φ)|2∈[1,4],
∴| ![]() +
+ ![]() |∈[1,2].
|∈[1,2].
(2)解: ![]() =(2sinx,cosx+k),
=(2sinx,cosx+k),
g(x)=( ![]() )
) ![]()
=﹣4sinxcosx+(cosx+k)(sinx﹣k)
=﹣3sinxcosx+k(sinx﹣cosx)﹣k2
令t=sinx﹣cosx= ![]() sin(x﹣
sin(x﹣ ![]() ),
),
则t∈[﹣ ![]() ,
, ![]() ],且t2=sin2x+cos2x﹣2sinxcosx=1﹣2sinxcosx,
],且t2=sin2x+cos2x﹣2sinxcosx=1﹣2sinxcosx,
所以 ![]() .
.
所以g(x)可化为 ![]() ,
,
对称轴 ![]() .
.
①当 ![]() ,即
,即 ![]() 时,
时, ![]() ,
,
由 ![]() ,得
,得 ![]() ,
,
所以 ![]() .
.
因为 ![]() ,
,
所以此时无解.
②当 ![]() ,即
,即 ![]() 时,
时, ![]() .
.
由﹣ ![]() ﹣
﹣ ![]() =﹣
=﹣ ![]() ,得k=0∈[﹣3
,得k=0∈[﹣3 ![]() ,3
,3 ![]() ].
].
③当﹣ ![]() ,即k<﹣3
,即k<﹣3 ![]() 时,
时,
g(x)min=h( ![]() )=﹣k2+
)=﹣k2+ ![]() k+
k+ ![]() ,
,
由﹣k2+ ![]() k+
k+ ![]() =﹣
=﹣ ![]() ,得k2﹣
,得k2﹣ ![]() k﹣3=0,
k﹣3=0,
所以k= ![]() .
.
因为k ![]() ,所以此时无解.
,所以此时无解.
综上所述,当k=0时,g(x)的最小值为﹣ ![]() .
.
【解析】(1)由已知利用平面向量的坐标运算可得 ![]() =(sinx﹣2cosx,sinx),利用三角函数恒等变换的应用可得|
=(sinx﹣2cosx,sinx),利用三角函数恒等变换的应用可得| ![]() |2=
|2= ![]() cos(2x+φ)+3,其中,tanφ=2,又x∈[0,
cos(2x+φ)+3,其中,tanφ=2,又x∈[0, ![]() ],可求
],可求 ![]() ,利用余弦函数的单调性即可得解|
,利用余弦函数的单调性即可得解| ![]() +
+ ![]() |的取值范围;(2)利用平面向量数量积的运算可得g(x)=﹣3sinxcosx+k(sinx﹣cosx)﹣k2 , 令t=sinx﹣cosx=
|的取值范围;(2)利用平面向量数量积的运算可得g(x)=﹣3sinxcosx+k(sinx﹣cosx)﹣k2 , 令t=sinx﹣cosx= ![]() sin(x﹣
sin(x﹣ ![]() ),则g(x)可化为
),则g(x)可化为 ![]() ,对称轴
,对称轴 ![]() .利用二次函数的图象和性质分类讨论即可得解.
.利用二次函数的图象和性质分类讨论即可得解.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:
【题目】2016年10月,继微信支付对提现转账收费后,支付宝也开始对提现转账收费,随着这两大目前用户使用粘度最高的第三方支付开始收费,业内人士分析,部分对价格敏感的用户或将回流至传统银行体系,某调查机构对此进行调查,并从参与调查的数万名支付宝用户中随机选取200人,把这200人分为3类:认为使用支付宝方便,仍使用支付宝提现转账的用户称为“![]() 类用户”;根据提现转账的多少确定是否使用支付宝的用户称为“
类用户”;根据提现转账的多少确定是否使用支付宝的用户称为“![]() 类用户”;提前将支付宝账户内的资金全部提现,以后转账全部通过银行的用户称为“
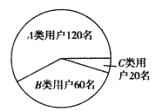
类用户”;提前将支付宝账户内的资金全部提现,以后转账全部通过银行的用户称为“![]() 类用户”,各类用户的人数如图所示:
类用户”,各类用户的人数如图所示:
同时把这200人按年龄分为青年人组与中老年人组,制成如图所示的![]() 列联表:
列联表:
| 非 | 合计 | |
青年 | 20 | ||
中老年 | 40 | ||
合计 | 200 |
(Ⅰ)完成![]() 列联表并判断是否有99.5%的把握认为“
列联表并判断是否有99.5%的把握认为“![]() 类用户与年龄有关”;
类用户与年龄有关”;
(Ⅱ)从这200人中按![]() 类用户、
类用户、![]() 类用户、
类用户、![]() 类用户进行分层抽样,从中抽取10人,再从这10人中随机抽取4人,求在这4人中
类用户进行分层抽样,从中抽取10人,再从这10人中随机抽取4人,求在这4人中![]() 类用户、
类用户、![]() 类用户、
类用户、![]() 类用户均存在的概率;
类用户均存在的概率;
(Ⅲ)把频率作为概率,从支付宝所有用户(人数很多)中随机抽取3人,用![]() 表示所选3人中
表示所选3人中![]() 类用户的人数,求
类用户的人数,求![]() 的分布列与期望.
的分布列与期望.
附:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】生产甲乙两种元件,其质量按检测指标划分为:指标大于或者等于82为正品,小于82为次品,现随机抽取这两种元件各100件进行检测,检测结果统计如下:
测试指标 |
|
|
|
|
|
元件甲 | 8 | 12 | 40 | 32 | 8 |
元件乙 | 7 | 18 | 40 | 29 | 6 |
(1)试分别估计元件甲、乙为正品的概率;
(2)生产一件元件甲,若是正品可盈利40元,若是次品则亏损5元,生产一件元件乙,若是正品可盈利50元,若是次品则亏损10元.在(1)的前提下:
(i)记![]() 为生产1件甲和1件乙所得的总利润,求随机变量
为生产1件甲和1件乙所得的总利润,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(ii)求生产5件元件乙所获得的利润不少于140元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)= ![]() x3﹣
x3﹣ ![]() ax2+(a﹣1)x+1在区间(2,3)内为减函数,在区间(5,+∞)为增函数,则实数a的取值范围是( )
ax2+(a﹣1)x+1在区间(2,3)内为减函数,在区间(5,+∞)为增函数,则实数a的取值范围是( )
A.[3,4]
B.[5,7]
C.[4,6]
D.[7,8]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知右焦点为![]() 的椭圆
的椭圆![]() 关于直线
关于直线![]() 对称的图形过坐标原点.
对称的图形过坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 且不垂直于
且不垂直于![]() 轴的直线与椭圆
轴的直线与椭圆![]() 交于两点
交于两点![]() ,点
,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() .证明:直线
.证明:直线![]() 与
与![]() 轴的交点为
轴的交点为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从2 012名学生中选取50名学生参加数学竞赛,若采用下面的方法选取:先用简单随机抽样从2 012人中剔除12人,剩下的2 000人再按系统抽样的方法抽取50人,则在2 012人中,每人入选的概率( )
A.不全相等
B.均不相等
C.都相等,且为 ![]()
D.都相等,且为 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数x(个) | 2 | 3 | 4 | 5 |
加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
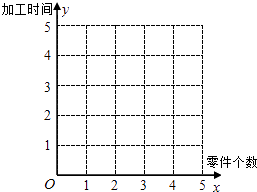
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出y关于x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;
(3)试预测加工10个零件需要多少时间? 参考公式:回归直线 ![]() =bx+a,其中b=
=bx+a,其中b= 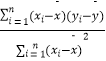 =
= 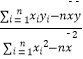 ,a=
,a= ![]() ﹣b
﹣b ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】二次函数f(x)=ax2+2a是区间[﹣a,a2]上的偶函数,又g(x)=f(x﹣1),则g(0),g( ![]() ),g(3)的大小关系是( )
),g(3)的大小关系是( )
A.g( ![]() )<g(0)<g(3)
)<g(0)<g(3)
B.g(0)<g( ![]() )<g(3)??
)<g(3)??
C.g( ![]() )<g(3)<g(0)
)<g(3)<g(0)
D.g(3)<g( ![]() )<g(0)
)<g(0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com