
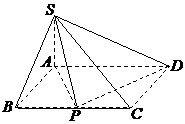
如图,四棱锥![]() 的底面是矩形,
的底面是矩形,![]() 底面
底面![]() ,P为BC边的中点,SB与平面ABCD所成的角为45°,且AD=2,SA=1.
,P为BC边的中点,SB与平面ABCD所成的角为45°,且AD=2,SA=1.
(1)求证:![]() 平面SAP;
平面SAP;
(2)求二面角A-SD-P的大小.
(2) ![]()
证明:(1)因为![]() 底面
底面![]() ,
,
所以,∠SBA是SB与平面ABCD所成的角…………………….……….1分
由已知∠SBA=45°,所以AB=SA=1
易求得,AP=PD=![]() ,…………………………………….…..………….2分
,…………………………………….…..………….2分
又因为AD=2,所以AD2=AP2+PD2,所以![]() .………….…….3分
.………….…….3分
因为SA⊥底面ABCD,![]() 平面ABCD,
平面ABCD,
所以SA⊥PD, …………….……………………….…....4分
由于SA∩AP=A 所以![]() 平面SAP. …………………………….5分
平面SAP. …………………………….5分
(2)设Q为AD的中点,连结PQ, ……………………………….………6分
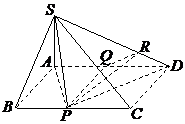 由于SA⊥底面ABCD,且SA
由于SA⊥底面ABCD,且SA![]() 平面SAD,则平面SAD⊥平面PAD……..7分
平面SAD,则平面SAD⊥平面PAD……..7分
因为PQ⊥AD,所以PQ⊥平面SAD
过Q作QR⊥SD,垂足为R,连结PR,
由三垂线定理可知PR⊥SD,
所以∠PRQ是二面角A-SD-P的平面角. …9分
容易证明△DRQ∽△DAS,则![]()
因为DQ=1,SA=1,![]() ,所以
,所以![]() ….……….10分
….……….10分
在Rt△PRQ中,因为PQ=AB=1,所以![]() ………11分
………11分
所以二面角A-SD-P的大小为![]() .……………….…….…….12分
.……………….…….…….12分
或:过A在平面SAP内作![]() ,且垂足为H,在平面SAD内作
,且垂足为H,在平面SAD内作![]() ,且垂足为E,连接HE,
,且垂足为E,连接HE,![]()
![]() 平面SAP。
平面SAP。![]()
![]() 平面SDP…………7分
平面SDP…………7分
∴HE为AE在平面SPD内的射影,∴由三垂线定理得![]()
从而![]() 是二面角A-SD-P的平面角……………………………….9分
是二面角A-SD-P的平面角……………………………….9分
在![]() 中,
中,![]() ,在
,在![]() 中,
中,![]() ,
,
![]()
![]() . ………………………………….11分
. ………………………………….11分
即二面角![]() 的大小为
的大小为![]() ……………………………12分
……………………………12分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
(09年山东实验中学诊断三理)(13分)如图:四棱锥![]() 的底面
的底面![]() 是提醒,腰
是提醒,腰![]() ,
,![]() 平分
平分![]() 且与
且与![]() 垂直,侧面
垂直,侧面![]() 都垂直于底面,平面
都垂直于底面,平面![]() 与底面
与底面![]() 成60°角
成60°角
![]() (1)求证:
(1)求证:![]() ;
;
![]() (2)求二面角
(2)求二面角![]() 的大小
的大小![]()
![]()
![]()
查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省高三第八次月考文科数学试卷 题型:解答题
如图,四棱锥 的底面是平行四边形,
的底面是平行四边形,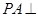 平面
平面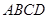 ,
,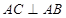 ,
,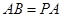 ,
,
点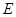 是
是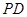 上的点,且
上的点,且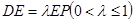 .
.
(Ⅰ)求证: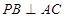 ;
;
(Ⅱ)求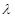 的值,使
的值,使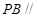 平面
平面 ;
;
(Ⅲ)当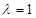 时,求三棱锥
时,求三棱锥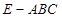 与四棱锥
与四棱锥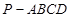 的体积之比.
的体积之比.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省高三上学期摸底理科数学 题型:解答题
((本小题满分14分)如图,四棱锥 的底面
的底面 是正方形,侧棱
是正方形,侧棱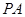
 底面
底面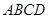 ,
,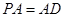 ,
,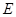 、
、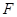 分别是棱
分别是棱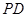 、
、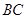 的中点.
的中点.
(1)求证: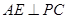 ; (2) 求直线
; (2) 求直线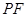 与平面
与平面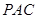 所成的角的正切值
所成的角的正切值
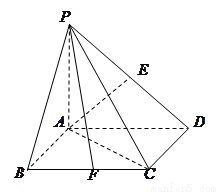
查看答案和解析>>
科目:高中数学 来源:2010-2011年四川省成都市高二3月月考数学试卷 题型:填空题
(本小题满分12 分)
如图,四棱锥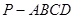 的底面是边长为
的底面是边长为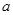 的菱形,
的菱形,
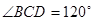 ,
,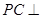 平面
平面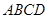 ,
,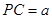 ,
,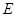 为
为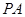 的中点,O为底面对角线的交点;
的中点,O为底面对角线的交点;
(1)求证:平面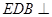 平面
平面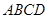 ;
;
(2)求二面角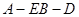 的正切值。
的正切值。
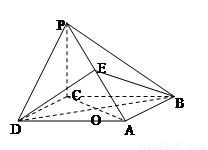
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com