
【题目】已知函数![]() 的定义域为
的定义域为![]() ,若存在区间
,若存在区间![]() 使得
使得![]() :
:
(Ⅰ)![]() 在
在![]() 上是单调函数;
上是单调函数;
(Ⅱ)![]() 在
在![]() 上的值域是
上的值域是![]() ,
,
则称区间![]() 为函数
为函数![]() 的“倍值区间”.
的“倍值区间”.
下列函数中存在“倍值区间”的有______________(填上所有你认为正确的序号)
①![]() ; ②
; ②![]() ;
;
③![]() ; ④
; ④![]() .
.
科目:高中数学 来源: 题型:
【题目】有一款击鼓小游戏规则如下:每盘游戏都需要击鼓三次,每次击鼓要么出现一次音乐,要么不出现音乐;每盘游戏击鼓三次后,出现一次音乐获得10分,出现两次音乐获得20分,出现三次音乐获得50分,没有出现音乐则扣除150分(即获得-150分).设每次击鼓出现音乐的概率为![]() ,且各次击鼓出现音乐相互独立.
,且各次击鼓出现音乐相互独立.
(Ⅰ)玩一盘游戏,至少出现一次音乐的概率是多少?
(Ⅱ)设每盘游戏获得的分数为![]() ,求
,求![]() 的分布列;
的分布列;
(Ⅲ)许多玩过这款游戏的人都发现,玩的盘数越多,分数没有增加反而减少了.请运用概率统计的相关知识分析其中的道理.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班上午有五节课,分別安排语文,数学,英语,物理,化学各一节课.要求语文与化学相邻,数学与物理不相邻,且数学课不排第一节,则不同排课法的种数是
A. 24B. 16C. 8D. 12
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为![]() =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是
A. y与x具有正的线性相关关系
B. 回归直线过样本点的中心(![]() ,
,![]() )
)
C. 若该大学某女生身高增加1cm,则其体重约增加0.85kg
D. 若该大学某女生身高为170cm,则可断定其体重比为58.79kg
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,
(1)求![]() 的解析式;
的解析式;
(2)关于![]() 的不等式
的不等式![]() 的解集为一切实数,求实数
的解集为一切实数,求实数![]() 的取值范围;
的取值范围;
(3)关于![]() 的不等式
的不等式![]() 的解集中的正整数解恰有
的解集中的正整数解恰有![]() 个,求实数
个,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把边长为a的等边三角形铁皮剪去三个相同的四边形(如图阴影部分)后,用剩余部分做成一个无盖的正三棱柱形容器(不计接缝),设容器的高为x,容积为![]() .
.
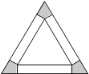
(1)写出函数![]() 的解析式,并求出函数的定义域;
的解析式,并求出函数的定义域;
(2)求当x为多少时,容器的容积最大?并求出最大容积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com