
【题目】已知边长为1的正方形 ![]() 与
与 ![]() 所在的平面互相垂直,点
所在的平面互相垂直,点 ![]() 分别是线段
分别是线段 ![]() 上的动点(包括端点),
上的动点(包括端点), ![]() ,设线段
,设线段 ![]() 的中点的轨迹为
的中点的轨迹为 ![]() ,则
,则 ![]() 的长度为( )
的长度为( )
A.![]()
B.![]()
C.![]()
D.2
【答案】A
【解析】如图,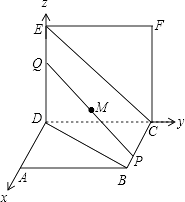
以DA、DC、DE所在直线分别为x、y、z轴建立空间直角坐标系,
设P(s,1,0)(0≤s≤1),Q(0,0,t)(0≤t≤1),M(x,y,z),
由中点坐标公式易知: ![]() ,即s=2x,t=2z ①,
,即s=2x,t=2z ①,
∵|PQ|= ![]() ,
,
∴s2+t2=1 ②,
把①代入②得,4x2+4z2=1.
即 ![]() .
.
∵0≤s≤1,0≤t≤1,
∴ ![]() .
.
∴PQ中点M的轨迹方程为 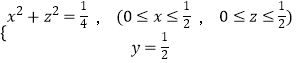 .
.
轨迹l为在垂直于y轴且距原点 ![]() 的平面内,半径为
的平面内,半径为 ![]() 的四分之一圆周.
的四分之一圆周.
∴l的长度为 ![]() .
.
所以答案是:A.
【考点精析】根据题目的已知条件,利用圆的标准方程的相关知识可以得到问题的答案,需要掌握圆的标准方程:![]() ;圆心为A(a,b),半径为r的圆的方程.
;圆心为A(a,b),半径为r的圆的方程.


科目:高中数学 来源: 题型:
【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对30名六年级学生进行了问卷调查,得到如下列联表(平均每天喝500ml以上为常喝,体重超过50kg为肥胖):
常喝 | 不常喝 | 合计 | |
肥胖 | 2 | ||
不肥胖 | 18 | ||
合计 | 30 |
已知在全部30人中随机抽取1人,抽到肥胖的学生的概率为 ![]() .
.
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由;
(3)现从常喝碳酸饮料且肥胖的学生中(2名女生),抽取2人参加电视节目,则正好抽到一男一女的概率是多少
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:K2= ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=exlnx(x>0),若对 ![]() 使得方程f(x)=k有解,则实数a的取值范围是( )
使得方程f(x)=k有解,则实数a的取值范围是( )
A.(0,ee]
B.[ee , +∞)
C.[e,+∞)
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,点 ![]() ,圆F2:x2+y2﹣2
,圆F2:x2+y2﹣2 ![]() x﹣13=0,以动点P为圆心的圆经过点F1 , 且圆P与圆F2内切.
x﹣13=0,以动点P为圆心的圆经过点F1 , 且圆P与圆F2内切.
(1)求动点的轨迹的方程;
(2)若直线l过点(1,0),且与曲线E交于A,B两点,则在x轴上是否存在一点D(t,0)(t≠0),使得x轴平分∠ADB?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin(ωx+)﹣1(ω>0,|φ|<π)的一个零点是 ![]() ,其图象上一条对称轴方程为
,其图象上一条对称轴方程为 ![]() ,则当ω取最小值时,下列说法正确的是 . (填写所有正确说法的序号) ①当
,则当ω取最小值时,下列说法正确的是 . (填写所有正确说法的序号) ①当 ![]() 时,函数f(x)单调递增;
时,函数f(x)单调递增;
②当 ![]() 时,函数f(x)单调递减;
时,函数f(x)单调递减;
③函数f(x)的图象关于点 ![]() 对称;
对称;
④函数f(x)的图象关于直线 ![]() 对称.
对称.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com