
ЁОЬтФПЁПвбжЊФГЕиЧјФГжжРЅГцВњТбЪ§КЭЮТЖШгаЙи.ЯжЪеМЏСЫвЛжЛИУЦЗжжРЅГцЕФВњТбЪ§![]() ЃЈИіЃЉКЭЮТЖШ
ЃЈИіЃЉКЭЮТЖШ![]() ЃЈ
ЃЈ![]() ЃЉЕФ7зщЙлВтЪ§ОнЃЌЦфЩЂЕуЭМШчЫљЪОЃК
ЃЉЕФ7зщЙлВтЪ§ОнЃЌЦфЩЂЕуЭМШчЫљЪОЃК
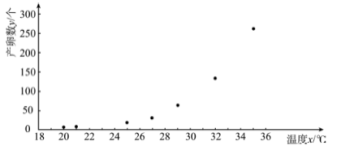
ИљОнЩЂЕуЭМЃЌНсКЯКЏЪ§жЊЪЖЃЌПЩвдЗЂЯжВњТбЪ§![]() КЭЮТЖШ
КЭЮТЖШ![]() ПЩгУЗНГЬ
ПЩгУЗНГЬ![]() РДФтКЯЃЌСю
РДФтКЯЃЌСю![]() ЃЌНсКЯбљБОЪ§ОнПЩжЊ
ЃЌНсКЯбљБОЪ§ОнПЩжЊ![]() гыЮТЖШ
гыЮТЖШ![]() ПЩгУЯпадЛиЙщЗНГЬРДФтКЯЃЎИљОнЪеМЏЕНЕФЪ§ОнЃЌМЦЫуЕУЕНШчЯТжЕЃК
ПЩгУЯпадЛиЙщЗНГЬРДФтКЯЃЎИљОнЪеМЏЕНЕФЪ§ОнЃЌМЦЫуЕУЕНШчЯТжЕЃК
|
|
|
|
|
|
27 | 74 |
| 182 |
|
|
Бэжа![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓ![]() КЭЮТЖШ
КЭЮТЖШ![]() ЕФЛиЙщЗНГЬЃЈЛиЙщЯЕЪ§НсЙћОЋШЗЕН
ЕФЛиЙщЗНГЬЃЈЛиЙщЯЕЪ§НсЙћОЋШЗЕН![]() ЃЉЃЛ
ЃЉЃЛ
ЃЈ2ЃЉЧѓВњТбЪ§![]() ЙигкЮТЖШ
ЙигкЮТЖШ![]() ЕФЛиЙщЗНГЬЃЛШєИУЕиЧјвЛЖЮЪБМфФкЕФЦјЮТдк
ЕФЛиЙщЗНГЬЃЛШєИУЕиЧјвЛЖЮЪБМфФкЕФЦјЮТдк![]() жЎМфЃЈАќРЈ
жЎМфЃЈАќРЈ![]() гы
гы![]() ЃЉЃЌЙРМЦИУЦЗжжвЛжЛРЅГцЕФВњТбЪ§ЕФЗЖЮЇ.ЃЈВЮПМЪ§ОнЃК
ЃЉЃЌЙРМЦИУЦЗжжвЛжЛРЅГцЕФВњТбЪ§ЕФЗЖЮЇ.ЃЈВЮПМЪ§ОнЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎЃЉ
ЃЎЃЉ
ИНЃКЖдгквЛзщЪ§Он![]() ЃЌ
ЃЌ![]() ЃЌЁЃЌ
ЃЌЁЃЌ![]() ЃЌЦфЛиЙщжБЯп
ЃЌЦфЛиЙщжБЯп![]() ЕФаБТЪКЭНиОрЕФзюаЁЖўГЫЙРМЦЗжБ№ЮЊ
ЕФаБТЪКЭНиОрЕФзюаЁЖўГЫЙРМЦЗжБ№ЮЊ ЃЎ
ЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЌ
ЃЌ![]() .
.
ЁОНтЮіЁП
(1)ИљОнЙЋЪНМЦЫуГі![]() КЭ
КЭ![]() ,ПЩЕУ
,ПЩЕУ![]() ;
;
(2)ИљОн![]() ПЩЕУ
ПЩЕУ![]() ,дйИљОнКЏЪ§
,дйИљОнКЏЪ§![]() ЮЊдіКЏЪ§ПЩЕУД№АИ.
ЮЊдіКЏЪ§ПЩЕУД№АИ.
ЃЈ1ЃЉвђЮЊ![]() гыЮТЖШ
гыЮТЖШ![]() ПЩвдгУЯпадЛиЙщЗНГЬРДФтКЯЃЌЩш
ПЩвдгУЯпадЛиЙщЗНГЬРДФтКЯЃЌЩш![]() ЃЎ
ЃЎ
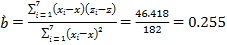 ЃЌ
ЃЌ
Ыљвд![]() ЃЌ
ЃЌ
ЙЪ![]() Йигк
Йигк![]() ЕФЯпадЛиЙщЗНГЬЮЊ
ЕФЯпадЛиЙщЗНГЬЮЊ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉгЩЃЈ1ЃЉПЩЕУ![]() ЃЌ
ЃЌ
гкЪЧВњТбЪ§![]() ЙигкЮТЖШ
ЙигкЮТЖШ![]() ЕФЛиЙщЗНГЬЮЊ
ЕФЛиЙщЗНГЬЮЊ![]() ,
,
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛ
ЃЛ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛ
ЃЛ
вђЮЊКЏЪ§![]() ЮЊдіКЏЪ§ЃЌ
ЮЊдіКЏЪ§ЃЌ
ЫљвдЃЌЦјЮТдк![]() жЎМфЪБЃЌвЛжЛИУЦЗжжРЅГцЕФВњТбЪ§ЕФЙРМЦЗЖЮЇЪЧ
жЎМфЪБЃЌвЛжЛИУЦЗжжРЅГцЕФВњТбЪ§ЕФЙРМЦЗЖЮЇЪЧ![]() ФкЕФе§ећЪ§ЃЎ
ФкЕФе§ећЪ§ЃЎ


 УћаЃСЗПМОэЦкФЉГхДЬОэЯЕСаД№АИ
УћаЃСЗПМОэЦкФЉГхДЬОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшЕу![]() ЃЌ
ЃЌ![]() ЗжБ№ЪЧЭждВ
ЗжБ№ЪЧЭждВ![]() :
:![]()
![]() ЕФзѓЁЂгвНЙЕуЃЌЧвЭждВ
ЕФзѓЁЂгвНЙЕуЃЌЧвЭждВ![]() ЩЯЕФЕуЕНЕу
ЩЯЕФЕуЕНЕу![]() ЕФОрРыЕФзюаЁжЕЮЊ
ЕФОрРыЕФзюаЁжЕЮЊ![]() .ЕуMЁЂNЪЧЭждВ
.ЕуMЁЂNЪЧЭждВ![]() ЩЯЮЛгк
ЩЯЮЛгк![]() жсЩЯЗНЕФСНЕуЃЌЧвЯђСП
жсЩЯЗНЕФСНЕуЃЌЧвЯђСП![]() гыЯђСП
гыЯђСП![]() ЦНаа.
ЦНаа.
ЃЈ1ЃЉЧѓЭждВ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌЧѓЁї
ЪБЃЌЧѓЁї![]() ЕФУцЛ§ЃЛ
ЕФУцЛ§ЃЛ
ЃЈ3ЃЉЕБ![]() ЪБЃЌЧѓжБЯп
ЪБЃЌЧѓжБЯп![]() ЕФЗНГЬ.
ЕФЗНГЬ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯп![]() ЃК
ЃК![]() ЩЯвЛЕу
ЩЯвЛЕу![]() ЕНЦфНЙЕу
ЕНЦфНЙЕу![]() ЕФОрРыЮЊ5.
ЕФОрРыЮЊ5.
ЃЈ1ЃЉЧѓ![]() гы
гы![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЩшЖЏжБЯп![]() гыХзЮяЯп
гыХзЮяЯп![]() ЯрНЛгк
ЯрНЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЌЮЪЃКдк
СНЕуЃЌЮЪЃКдк![]() жсЩЯЪЧЗёДцдкгы
жсЩЯЪЧЗёДцдкгы![]() ЕФШЁжЕЮоЙиЕФЖЈЕу
ЕФШЁжЕЮоЙиЕФЖЈЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЃПШєДцдкЃЌЧѓГіЕу
ЃПШєДцдкЃЌЧѓГіЕу![]() ЕФзјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩ.
ЕФзјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉЃНex![]() ЃЈxЉaЃЉ2+4ЃЎ
ЃЈxЉaЃЉ2+4ЃЎ
ЃЈ1ЃЉШєfЃЈxЃЉдкЃЈЉЁоЃЌ+ЁоЃЉЩЯЕЅЕїЕндіЃЌЧѓaЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉШєxЁн0ЃЌВЛЕШЪНfЃЈxЃЉЁн0КуГЩСЂЃЌЧѓaЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫФРтзЖ![]() жаЃЌЕзУц
жаЃЌЕзУц![]() ЮЊе§ЗНаЮЃЌ
ЮЊе§ЗНаЮЃЌ![]() ЕзУц
ЕзУц![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЕФжаЕуЃЎ
ЕФжаЕуЃЎ
ЃЈ1ЃЉШє![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЩЯЕФЖЏЕуЃЌжЄУїЃКЦНУц
ЩЯЕФЖЏЕуЃЌжЄУїЃКЦНУц![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШє![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЩЯЕФЖЏЕуЃЈВЛКЌ
ЩЯЕФЖЏЕуЃЈВЛКЌ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ![]() ЃЌШ§РтзЖ
ЃЌШ§РтзЖ![]() ЕФЬхЛ§ЪЧЗёДцдкзюДѓжЕЃПШчЙћДцдкЃЌЧѓГізюДѓжЕЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФЬхЛ§ЪЧЗёДцдкзюДѓжЕЃПШчЙћДцдкЃЌЧѓГізюДѓжЕЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌЦфжа
ЃЌЦфжа![]() ЃЌ
ЃЌ![]() ЮЊздШЛЖдЪ§ЕФЕзЪ§.
ЮЊздШЛЖдЪ§ЕФЕзЪ§.
ЃЈЂёЃЉЩш![]() ЪЧКЏЪ§
ЪЧКЏЪ§![]() ЕФЕМКЏЪ§ЃЌЧѓКЏЪ§
ЕФЕМКЏЪ§ЃЌЧѓКЏЪ§![]() дкЧјМф
дкЧјМф![]() ЩЯЕФзюаЁжЕЃЛ
ЩЯЕФзюаЁжЕЃЛ
ЃЈЂђЃЉШє![]() ЃЌКЏЪ§
ЃЌКЏЪ§![]() дкЧјМф
дкЧјМф![]() ФкгаСуЕуЃЌЧѓ
ФкгаСуЕуЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇ
ЕФШЁжЕЗЖЮЇ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() .
.
(1)ЧѓЧњЯп![]() дкЕу
дкЕу![]() ДІЕФЧаЯпЗНГЬЃЛ
ДІЕФЧаЯпЗНГЬЃЛ
(2)жЄУїЃК![]() дкЧјМф
дкЧјМф![]() ЩЯгаЧвНіга
ЩЯгаЧвНіга![]() ИіСуЕу.
ИіСуЕу.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
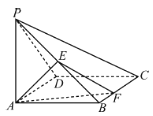
ЁОЬтФПЁПШчЭМЃЌдкжБШ§РтжљABCЃA1B1C1жаЃЌDЃЌEЗжБ№ЮЊBCЃЌACЕФжаЕуЃЌAB=BCЃЎ

ЧѓжЄЃКЃЈ1ЃЉA1B1ЁЮЦНУцDEC1ЃЛ
ЃЈ2ЃЉBEЁЭC1EЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгавдЯТУќЬтЃК
ЂйШєКЏЪ§fЃЈxЃЉМШЪЧЦцКЏЪ§гжЪЧХМКЏЪ§ЃЌдђfЃЈxЃЉЕФжЕгђЮЊ{0}ЃЛ
ЂкШєКЏЪ§fЃЈxЃЉЪЧХМКЏЪ§ЃЌдђfЃЈ|x|ЃЉ=fЃЈxЃЉЃЛ
ЂлШєКЏЪ§fЃЈxЃЉдкЦфЖЈвхгђФкВЛЪЧЕЅЕїКЏЪ§ЃЌдђfЃЈxЃЉВЛДцдкЗДКЏЪ§ЃЛ
ЂмШєКЏЪ§fЃЈxЃЉДцдкЗДКЏЪ§fЉ1ЃЈxЃЉЃЌЧвfЉ1ЃЈxЃЉгыfЃЈxЃЉВЛЭъШЋЯрЭЌЃЌдђfЃЈxЃЉгыfЉ1ЃЈxЃЉЭМЯѓЕФЙЋЙВЕуБидкжБЯпy=xЩЯЃЛ
ЦфжаецУќЬтЕФађКХЪЧ ЃЎЃЈаДГіЫљгаецУќЬтЕФађКХЃЉ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com