
【题目】在平面立角坐标系![]() 中,过点
中,过点![]() 的圆的圆心
的圆的圆心![]() 在
在![]() 轴上,且与过原点倾斜角为
轴上,且与过原点倾斜角为![]() 的直线
的直线![]() 相切.
相切.
(1)求圆![]() 的标准方程;
的标准方程;
(2)点![]() 在直线
在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线
的切线![]() 、
、![]() ,切点分别为
,切点分别为![]() 、
、![]() ,求经过
,求经过![]() 、
、![]() 、
、![]() 、
、![]() 四点的圆所过的定点的坐标.
四点的圆所过的定点的坐标.
【答案】(1)![]() (2)经过
(2)经过![]() 、
、![]() 、
、![]() 、
、![]() 四点的圆所过定点的坐标为
四点的圆所过定点的坐标为![]() 、
、![]()
【解析】
(1)先算出直线方程,根据相切和过点![]() ,圆心
,圆心![]() 在
在![]() 轴上联立方程解得答案.
轴上联立方程解得答案.
(2) 取线段![]() 的中点
的中点![]() ,经过
,经过![]() 、
、![]() 、
、![]() 、
、![]() 四点的圆是以线段
四点的圆是以线段![]() 为直径的圆,设点
为直径的圆,设点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 的坐标为
的坐标为![]() ,将圆方程表示出来,联立方程组解得答案.
,将圆方程表示出来,联立方程组解得答案.
(1)由题意知,直线![]() 的方程为
的方程为![]() ,整理为一般方程可得
,整理为一般方程可得![]()
由圆![]() 的圆心在
的圆心在![]() 轴上,可设圆
轴上,可设圆![]() 的方程为
的方程为![]() ,
,
由题意有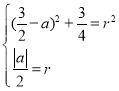 ,解得:
,解得:![]() ,
,![]() ,
,
故圆![]() 的标准方程为
的标准方程为![]() .
.
(2)由圆的几何性质知,![]() ,
,![]() ,取线段
,取线段![]() 的中点
的中点![]() ,由直角三角形的性质可知
,由直角三角形的性质可知![]() ,故经过
,故经过![]() 、
、![]() 、
、![]() 、
、![]() 四点的圆是以线段
四点的圆是以线段![]() 为直径的圆,
为直径的圆,
设点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 的坐标为
的坐标为![]()
有![]()
则以![]() 为直径的圆的方程为:
为直径的圆的方程为:![]() ,整理为
,整理为![]()
可得![]() .
.
令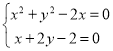 ,解得
,解得![]() 或
或![]() ,
,
故经过![]() 、
、![]() 、
、![]() 、
、![]() 四点的圆所过定点的坐标为
四点的圆所过定点的坐标为![]() 、
、![]() .
.


科目:高中数学 来源: 题型:
【题目】为了得到函数y=3cos2x的图象,只需把函数y=3sin(2x+ ![]() )的图象上所有的点( )
)的图象上所有的点( )
A.向右平行移动 ![]() 个单位长度
个单位长度
B.向右平行移动 ![]() 个单位长度
个单位长度
C.向左平行移动 ![]() 个单位长度
个单位长度
D.向左平移移动 ![]() 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心在![]() 轴的正半轴上,且半径为2的圆
轴的正半轴上,且半径为2的圆![]() 被直线
被直线![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)设动直线![]() 与圆
与圆![]() 交于
交于![]() 两点,则在
两点,则在![]() 轴正半轴上是否存在定点
轴正半轴上是否存在定点![]() ,使得直线
,使得直线![]() 与直线
与直线![]() 关于
关于![]() 轴对称?若存在,请求出点
轴对称?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极坐标系的极点与直角坐标系的原点重合,极轴与x轴的非负半轴重合,若曲线C1的方程为ρsin(θ+ ![]() )+2
)+2 ![]() =0,曲线C2的参数方程为
=0,曲线C2的参数方程为 ![]() (θ为参数).
(θ为参数).
(1)将C1的方程化为直角坐标方程;
(2)若点Q为C2上的动点,P为C1上的动点,求|PQ|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】土笋冻是闽南种广受欢迎的特色传统风味小吃某小区超市销售一款土笋冻,进价为每个15元,售价为每个20元.销售的方案是当天进货,当天销售,未售出的全部由厂家以每个10元的价格回购处理.根据该小区以往的销售情况,得到如图所示的频率分布直方图:

(1)估算该小区土笋冻日需求量的平均数![]() (同一组中的数据用该组区间的中点值代表);
(同一组中的数据用该组区间的中点值代表);
(2)已知该超市某天购进了150个土笋冻,假设当天的需求量为![]() 个
个![]() 销售利润为
销售利润为![]() 元.
元.
(i)求关于![]() 的函数关系式;
的函数关系式;
(ii)结合上述频率分布直方图,以额率估计概率的思想,估计当天利润![]() 不小于650元的概率.
不小于650元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某社区居民有无收看“奥运会开幕式”,某记者分别从某社区60~70岁,40~50岁,20~30岁的三个年龄段中的160人,240人,x人中,采用分层抽样的方法共抽查了30人进行调查,若在60~70岁这个年龄段中抽查了8人,那么x为( ) .
A. 90 B. 120 C. 180 D. 200
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]() .
.

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,求二面角A-PB-C的余弦值.
,求二面角A-PB-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《张丘建算经》是公元5世纪中国古代内容丰富的数学著作,书中卷上第二十三问:“今有女善织,日益功疾,初日织五尺,今一月织九匹三丈.问日益几何?”其意思为“有个女子织布,每天比前一天多织相同量的布,第一天织五尺,一个月(按30天计)共织390尺.问:每天多织多少布?”已知1匹=4丈,1丈=10尺,估算出每天多织的布的布约有( )
A.0.55尺
B.0.53尺
C.0.52尺
D.0.5尺
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com