
小明家订了一份报纸,寒假期间他收集了每天报纸送达时间的数据,并绘制成频率分布直方图,如图所示.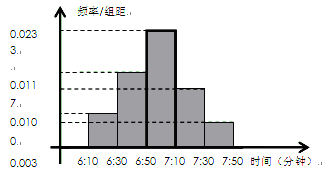
(1)根据图中的数据信息,求出众数 和中位数
和中位数 (精确到整数分钟);
(精确到整数分钟);
(2)小明的父亲上班离家的时间 在上午
在上午 之间,而送报人每天在
之间,而送报人每天在 时刻前后半小时内把报纸送达(每个时间点送达的可能性相等),求小明的父亲在上班离家前能收到报纸(称为事件
时刻前后半小时内把报纸送达(每个时间点送达的可能性相等),求小明的父亲在上班离家前能收到报纸(称为事件 )的概率.
)的概率.
(1) ,
, ;(2)
;(2)
解析试题分析:(1)在频率分步直方图中,最高矩形的中点横坐标代表数据的众数;各个矩形的面积和为1,中位数是面积等分为 的轴线和横轴的交点;平均数是各矩形的面积乘以相应矩形中点横坐标的累加值;(2)基本事件总数有无限多个,故可以考虑几何概型.
的轴线和横轴的交点;平均数是各矩形的面积乘以相应矩形中点横坐标的累加值;(2)基本事件总数有无限多个,故可以考虑几何概型.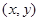 可以看成平面中的点,试验的全部结果构成平面区域
可以看成平面中的点,试验的全部结果构成平面区域 ,而事件A发生的前提是
,而事件A发生的前提是 ,利用面积的比表示事件A发生的概率
,利用面积的比表示事件A发生的概率 .
.
试题解析:(1) 2分
2分
由频率分布直方图可知 即
即 , 3分
, 3分
∴

解得 分即
分即 6分
6分
(2)设报纸送达时间为 7分
7分
则小明父亲上班前能取到报纸等价于 , 10分
, 10分
如图可知,所求概率为 13分
13分
考点:1、频率分布直方图;2、众数和中位数;3、几何概型.


科目:高中数学 来源: 题型:解答题
下表是某市从3月份中随机抽取的 天空气质量指数(
天空气质量指数( )和“
)和“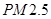 ”(直径小于等于
”(直径小于等于 微米的颗粒物)
微米的颗粒物) 小时平均浓度的数据,空气质量指数(
小时平均浓度的数据,空气质量指数( )小于
)小于 表示空气质量优良.
表示空气质量优良.
| 日期编号 |  |  |  |  |  |  |  |  |  |  |
空气质量指数( ) ) |  |  |  |  |  |  |  |  |  |  |
“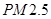 ” ” 小时平均浓度( 小时平均浓度(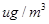 ) ) |  |  |  |  |  |  |  |  |  |  |
 为“抽取的两个日期中,当天‘
为“抽取的两个日期中,当天‘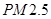 ’的
’的 小时平均浓度不超过
小时平均浓度不超过 ”,求事件
”,求事件 发生的概率.
发生的概率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某商店试销某种商品20天,获得如下数据:
| 日销售量(件) | 0 | 1 | 2 | 3 |
| 频数 | 1 | 5 | 9 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 .
.
(1)从区间 内任取一个实数
内任取一个实数 ,设事件
,设事件 ={函数
={函数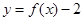 在区间
在区间 上有两个不同的零点},求事件
上有两个不同的零点},求事件 发生的概率;
发生的概率;
(2)若连续掷两次骰子(骰子六个面上标注的点数分别为 )得到的点数分别为
)得到的点数分别为 和
和 ,记事件
,记事件 {
{ 在
在 恒成立},求事件
恒成立},求事件 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两射手在同一条件下进行射击,分布列如下:射手甲击中环数8,9,10的概率分别为0.2,0.6,0.2;射手乙击中环数8,9,10的概率分别为0.4,0.2,0.4.用击中环数的期望与方差比较两名射手的射击水平.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
有一种闯三关游戏规则规定如下:用抛掷正四面体型骰子(各面上分别有1,2,3,4点数的质地均匀的正四面体)决定是否过关,在闯第n(n=1,2,3)关时,需要抛掷n次骰子,当n次骰子面朝下的点数之和大于n2时,则算闯此关成功,并且继续闯关,否则停止闯关.每次抛掷骰子相互独立.
(1)求仅闯过第一关的概率;
(2)记成功闯过的关数为ξ,求ξ的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某中学为丰富教工生活,国庆节举办教工趣味投篮比赛,有 、
、 两个定点投篮位置,在
两个定点投篮位置,在 点投中一球得2分,在
点投中一球得2分,在 点投中一球得3分.其规则是:按先
点投中一球得3分.其规则是:按先 后
后 再
再 的顺序投
的顺序投
篮.教师甲在 和
和 点投中的概率分别是
点投中的概率分别是 ,且在
,且在 、
、 两点投中与否相互独立.
两点投中与否相互独立.
(1)若教师甲投篮三次,试求他投篮得分X的分布列和数学期望;
(2)若教师乙与甲在A、B点投中的概率相同,两人按规则各投三次,求甲胜乙的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com