一个口袋中装有n个红球(n≥4且n∈N)和5个白球,从中摸两个球,两个球颜色相同则为中奖.
(Ⅰ)若一次摸两个球,试用n表示一次摸球中奖的概率p;
(Ⅱ)若一次摸一个球,当n=4时,求二次摸球(每次摸球后不放回)中奖的概率;
(Ⅲ)在(Ⅰ)的条件下,记三次摸奖(每次摸奖后放回)恰有二次中奖的概率为P,当n取多少时,P最大?
解:(Ⅰ)由题意知本题是一个等可能事件的概率,
试验发生包含的事件是一次摸奖从n+5个球中任选两个,有C
n+52种,
满足条件的事件是两球不同色有C
n1C
51种,
根据等可能事件的概率得到一次摸奖中奖的概率
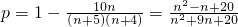
(Ⅱ)若n=4,由题意知本题是一个等可能事件的概率
试验发生包含的事件数C
81C
91,
满足条件的事件是C
41C
31+C
51C
41得到二次摸奖(每次摸奖后不放回)中奖的概率是
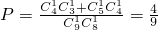
答:二次摸球(每次摸球后不放回)中奖的概率为

..
(Ⅲ)设每次摸奖中奖的概率为p,则三次摸奖(每次摸奖后放回)
恰有二次中奖的概率为P为P=P
3(2)=C
32•p
2•(1-p)=3(p
2-p
3),0<p<1,..
当

时,P取得最大值.
又
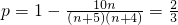
,解得n=20
答:当n=20时,三次摸奖(每次摸奖后放回)恰有二次中奖的概率最大
分析:(Ⅰ)本题是一个等可能事件的概率,试验发生包含的事件是一次摸奖从n+5个球中任选两个,满足条件的事件是两球不同色有C
n1C
51种,根据等可能事件的概率得到结果.
(Ⅱ)本题是一个等可能事件的概率,试验发生包含的事件数C
81C
91,满足条件的事件是C
41C
31+C
51C
41,根据等可能事件的概率得到结果.
(III)设每次摸奖中奖的概率为p,则三次摸奖(每次摸奖后放回),恰有二次中奖的概率为P为P=P
3(2)=C
32•p
2•(1-p)=3(p
2-p
3),当

时,P取得最大值.得到n的值.
点评:本题考查等可能事件的概率,考查等可能事件的概率的应用,这种问题可以出现在大型考试的解答题目中,是一个综合题.

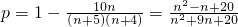
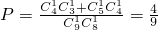
 ..
.. 时,P取得最大值.
时,P取得最大值.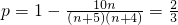 ,解得n=20
,解得n=20 时,P取得最大值.得到n的值.
时,P取得最大值.得到n的值.
