
设V为全体平面向量构成的集合,若映射f:
V→R满足:
对任意向量a=(x1,y1)∈V,b=(x2,y2)∈V,以及任意λ∈R,均有f[λa+(1-λ)b]=λf(a)+(1-λ)f(b),则称映射f具有性质p.
现给出如下映射:
①f1:V→R,f1(m)=x-y,m=(x,y)∈V;
②f2:V→R,f2(m)=x2+y,m=(x,y)∈V;
③f3:V→R,f3(m)=x+y+1,m=(x,y)∈V.
分析映射①②③是否具有性质p.
①具有性质p②不具有性质p. ③具有性质p.
【解析】a=(x1y1),b=(x2,y2),
λa+(1-λ)b=(λx1+(1-λ)x2,λy1+(1-λ)y2).
对于①,f1(m)=x-y
∴f(λa+(1-λ)b)=[λx1+(1-λ)x2]-[λy1+(1-λ)y2]
=λ(x1-y1)+(1-λ)(x2-y2).
λf(a)+(1-λ)f(b)=λ(x1-y1)+(1-λ)(x2-y2)
f(λa+(1-λ)b)=λf(a)+(1-λ)f(b).
∴①具有性质p.
对于②,f2(m)=x2+y,设a=(0,0),b=(1,2),
λa+(1-λ)b=(1-λ,2(1-λ)),
f(λa+(1-λ)b)=(1-λ)2+2(1-λ)=λ2-4λ+3,
而λf(a)+(1-λ)b=λ(02+0)+(1-λ)(12+2)=3(1-λ).
又λ∈R,∴f(λa+(1-λ)b)=λf(a)+(1-λ)f(b)不恒成立
故②不具有性质p.
对于③,f3(m)=x+y+1,
f(λa+(1-λ)b)=[λx1+(1-λ)x2]+[λy1+(1-λ)y2]+1
=λ(x1+y1)+(1-λ)(x2+y2)+1,
又λf(a)+(1-λ)f(b)=λ(x1+y1+1)+(1-λ)(x2+y2+1)
=λ(x1+y1)+(1-λ)(x2+y2)+λ+(1-λ)
=λ(x1+y1)+(1-λ)(x2+y2)+1.
∴f(λa+(1-λ)b)=λf(a)+(1-λ)f(b)
③具有性质p.


科目:高中数学 来源:2015届湘教版高二数学选修2-2基础达标6.3练习卷(解析版) 题型:解答题
已知,n∈N+,An=2n2,Bn=3n,试比较An与Bn的大小,
并加以证明.
查看答案和解析>>
科目:高中数学 来源:2015届湘教版高二数学选修2-2基础达标6.1练习卷(解析版) 题型:解答题
先阅读下列不等式的证法,再解决后面的问题:
已知a1,a2∈R,a1+a2=1,求证: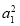 +
+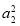 ≥
≥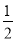 .
.
证明:构造函数f(x)=(x-a1)2+(x-a2)2,f(x)对一切实数x∈R,恒有f(x)≥0,则Δ=4-8(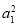 +
+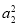 )≤0,∴
)≤0,∴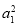 +
+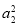 ≥
≥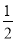 .
.
(1)已知a1,a2,…,an∈R,a1+a2+…+an=1,请写出上述结论的推广式;
(2)参考上述解法,对你推广的结论加以证明.
查看答案和解析>>
科目:高中数学 来源:2015届湘教版高二数学选修2-2基础达标6.1练习卷(解析版) 题型:解答题
在数列{an}中,a1=1,an+1=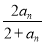 ,n∈N+,求a2,a3,a4
,n∈N+,求a2,a3,a4
并猜想数列的通项公式,并给出证明.
查看答案和解析>>
科目:高中数学 来源:2015届湘教版高二数学选修2-2基础达标6.1练习卷(解析版) 题型:填空题
n个连续自然数按规律排列下表:
0 3 → 4 7 → 8 11…
↓ ↑ ↓ ↑ ↓ ↑
1 → 2 5 → 6 9 → 10
根据规律,从2010到2012箭头方向依次为________.
查看答案和解析>>
科目:高中数学 来源:2015届湘教版高二数学选修2-2基础达标5章末练习卷(解析版) 题型:选择题
已知z是纯虚数,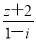 是实数,那么z等于 ( ).
是实数,那么z等于 ( ).
A.2i B.i C.-i D.-2i
查看答案和解析>>
科目:高中数学 来源:2015届湘教版高二数学选修2-2基础达标4章末练习卷(解析版) 题型:填空题
若曲线f(x)=ax3+ln x存在垂直于y轴的切线,则实数a的取值范围是
________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com