练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    对于任意正整数n，定义“n的双阶乘n!!”如下：

    当n是偶数时，n!!=n·(n-2)·(n-4)……6·4·2；

    当n是奇数时，n!!=n·(n-2)·(n-4)……5·3·1

    现在有如下四个命题：①(2003!!)·(2002!!)=2003!；②2002!!=21001·1001!；

    ③2002!!的个位数是0；　④2003!!的个位数是5.

    其中正确的命题有(    )

    （A）4个         （B）3个           （C）2个           （D）1个

     

    【答案】

    A

    【解析】解：因为当n是偶数时，n!!=n·(n-2)·(n-4)……6·4·2；

    当n是奇数时，n!!=n·(n-2)·(n-4)……5·3·1

    ①(2003!!)·(2002!!)=2003!；②2002!!=21001·1001!；

    ③2002!!的个位数是0；　④2003!!的个位数是5.

    炎症可知都满足公式成立。选A

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2002年全国各省市高考模拟试题汇编 题型：044

    已知函数y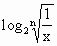＝(n∈N)．

    (Ⅰ)当n＝1，2，3…时，把已知函数的图像和直线y＝1的交点的横坐标依次记为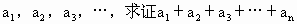＜1；

    (Ⅱ)对于每一个n的值，设为已知函数的图像上与x轴距离为1的两点，求证：n取任意一个正整数时，以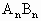为直径的圆都与一条定直线相切，并求出这条定直线的方程和切点的坐标．

    查看答案和解析>>

    科目：高中数学 来源：数学教研室 题型：044

        已知函数点P1(x1, y1)和P2(x2, y2)是f(x)的图象上的动点，且线段P1P2的中点P的坐标为.

    （I）求证：a是定值；

    （II）对于任意的正整数n，设试判断数列{Sn}是否为等差数列，若是，请加以证明；若不是，说明理由.

     

    查看答案和解析>>

    科目：高中数学 来源：成功之路·突破重点线·数学（学生用书） 题型：047

    已知函数y＝log2(n∈N*)．

    (1)当n＝1，2，3，…时，把已知函数的图象和直线y＝1的交点的横坐标依次记为a1，a2，a3，……，求证a1＋a2＋a3＋…＋an＜1；

    (2)对于每一个n的值，设An、Bn为已知函数的图象上与x轴距离为1的两点，求证：n取任意一个正整数时，以AnBn为直径的圆都与一条定直线相切，并求出这条定直线的方程和切点的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数 (n∈N*).?

    (1)当n=1,2,3,…时,把已知函数的图象和直线y=1的交点的横坐标依次记为a1,a2,a3,…,求证:a1+a2+…+an＜1;??

    (2)对于每一个n的值,设An、Bn为已知函数的图象上与x轴距离为1的两点,求证:n取任意一个正整数时,以AnBn为直径的圆都与一条定直线相切,并求出这条定直线的方程和切点的坐标.

    查看答案和解析>>

    同步练习册答案