练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    口袋中有n(n∈N*)个白球，3个红球．依次从口袋中任取一球，如果取到红球，那么继续取球，且取出的红球不放回；如果取到白球，就停止取球．记取球的次数为X.若P(X＝2)＝，则n的值为(  )

    A．5 B．6 C．7 D．8

    C

    解析试题分析：由题意知，当时，即第一次取到红球，其概率为，且不放回；第二次取到白球，其概率为，则，可解得或（舍），即.故选C.
    考点：排列数公式的应用.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    已知的二项展开式中所有奇数项的系数之和为512，
    （1）求展开式的所有有理项．
    （2）求展开式中项的系数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    设服从二项分布X～B（n，p）的随机变量X的均值与方差分别是15和，则n、p的值分别是（ ）

    A．50， B．60， C．50， D．60，

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    袋中有大小相同的三个白球和两个黑球，从中任取两个球，两球同色的概率为（  ）

    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    在长为12cm的线段AB上任取一点M，并以线段AM为一边作正方形，则此正方形的面积介于36cm2与81cm2之间的概率为（　　）

    A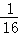． B． C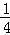． D． 

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    在独立性检验中，统计量有两个临界值：3．841和6．635；当3．841时，认为两个事件无关，当＞6．635时，有99%的把握说明两个事件有关．在一项打鼾与患心脏病的调查中，共调查了2000人，经计算的    =20．87，根据这一数据，认为打鼾与患心脏病之间（   ）

    A．认为两者无关B．约有95%的打鼾者患心脏病
    C．有99%的把握认为两者有关D．约有99%的打鼾者患心脏病

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    设随机变量服从正态分布，若，则的值为（   ）

    A． B． C．5 D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    在用0，1，2，3，4组成的没有重复数字的五位数中，
    （1）偶数有多少个；
    （2）个位上的数比十位上的数大的数有多少个；
    （3）数字1和2相邻，且3和4不相邻的数有多少个．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    某班50名学生期中考试数学成绩的频率分布直方图如图所示，其中成绩分组区间是：[40,50)，[50,60)，[60,70)，[70,80)，[80,90)，[90,100]．从样本成绩不低于80分的学生中随机选取2人，这2人中成绩在90分以上(含90分)的人数为ξ，则ξ的数学期望为(　　)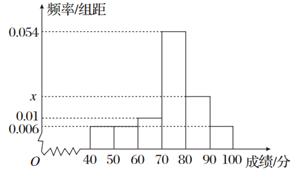

    A． B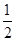． C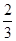． D．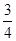

    查看答案和解析>>

    同步练习册答案