
| A. | (0,$\frac{3}{4}$) | B. | [$\frac{1}{2}$,$\frac{3}{4}$) | C. | ($\frac{1}{4}$,$\frac{1}{2}$) | D. | [$\frac{1}{4}$,$\frac{3}{4}$) |
分析 构造函数g(x)=mx+m-1,f(x)=$\sqrt{-{x}^{2}+4x-3}$,在同一坐标系中作出二函数的图象,数形结合即可求得实数m的取值范围.
解答 解:令g(x)=mx+m-1,f(x)=$\sqrt{-{x}^{2}+4x-3}$,
∵方程mx+3m=$\sqrt{-{x}^{2}+4x-3}$有两个不同的实数解,
∴g(x)=mx+m-1与f(x)=$\sqrt{-{x}^{2}+4x-3}$有两个不同的交点,
在同一坐标系中作图如下: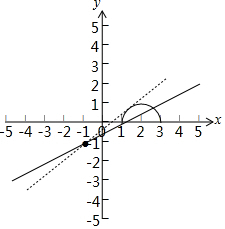
∵g(x)=mx+m-1为过定点(-1,-1)的直线,
当直线g(x)=mx+m-1经过(1,0),即m=$\frac{1}{2}$时,
显然g(x)=mx+m-1与f(x)=$\sqrt{-{x}^{2}+4x-3}$有两个不同的交点;
当直线g(x)=mx+m-1与曲线f(x)=$\sqrt{-{x}^{2}+4x-3}$相切时,
$\frac{|2m+m-1|}{\sqrt{{m}^{2}+1}}=1$,解得m=$\frac{3}{4}$或m=0(舍),
∴m∈[$\frac{1}{2}$,$\frac{3}{4}$),
故选:B
点评 本题考查根的存在性及根的个数判断,考查等价转化思想与数形结合思想的综合应用,属于中档题


科目:高中数学 来源: 题型:选择题
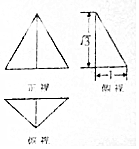 已知三棱锥的三视图如图所示,其中俯视图为直角三角形,俯视图为等腰直角三角形,则此三棱锥的体积等于( )
已知三棱锥的三视图如图所示,其中俯视图为直角三角形,俯视图为等腰直角三角形,则此三棱锥的体积等于( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
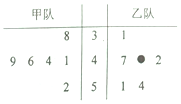 甲乙两个竞赛队都参加了6场比赛,比赛得分情况的经营如图如图(单位:分)),其中乙队的一个得分数字被污损,那么估计乙队的平均得分大于甲队的平均得分的概率为( )
甲乙两个竞赛队都参加了6场比赛,比赛得分情况的经营如图如图(单位:分)),其中乙队的一个得分数字被污损,那么估计乙队的平均得分大于甲队的平均得分的概率为( )| A. | $\frac{1}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
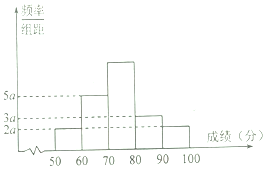 某学习小组20名学生一次数学考试成绩(单位:分)频率直方图如图所示,已知前三个矩形框垂直于横轴的高度成等差数列.
某学习小组20名学生一次数学考试成绩(单位:分)频率直方图如图所示,已知前三个矩形框垂直于横轴的高度成等差数列.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com