
分析 利用三角形的面积公式可得|PF1||PF2|=$\frac{4}{\sqrt{3}}$,由双曲线性质得出|PF1|-|PF2|=2n,代入余弦定理即可消去n得出关于m的方程.
解答 解:∵S${\;}_{△{F}_{1}P{F}_{2}}$=$\frac{1}{2}|P{F}_{1}||P{F}_{2}|sin∠{F}_{1}P{F}_{2}$=$\frac{\sqrt{3}}{4}$|PF1||PF2|=1,
∴|PF1||PF2|=$\frac{4}{\sqrt{3}}$.
∵P在双曲线上,∴|PF1|-|PF2|=2n,
∴|PF1|=2n+|PF2|,∴(2n+|PF2|)|PF2|=$\frac{4}{\sqrt{3}}$.
在△F1PF2中,由余弦定理得:|F1F2|2=|PF1|2+|PF2|2-2|PF1||PF2|cos∠F1PF2=|PF1|2+|PF2|2-|PF1||PF2|.
∵|F1F2|2=4c2=4m2+4n2,
∴4m2+4n2=(2n+|PF2|)2+|PF2|2-$\frac{4}{\sqrt{3}}$,
∴4m2=2|PF2|2+4n|PF2|-$\frac{4}{\sqrt{3}}$=2(2n+|PF2|)|PF2|-$\frac{4}{\sqrt{3}}$=$\frac{8}{\sqrt{3}}-\frac{4}{\sqrt{3}}=\frac{4}{\sqrt{3}}$.
∴m2=$\frac{1}{\sqrt{3}}$=$\sqrt{\frac{1}{3}}$,
∴m=$\root{4}{\frac{1}{3}}$.
故答案为:$\root{4}{\frac{1}{3}}$.
点评 本题考查了双曲线的简单性质,余弦定理,属于中档题.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$ | B. | 2$\sqrt{2}$ | C. | -2$\sqrt{2}$ | D. | -2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
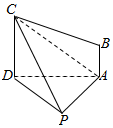 如图,已知平面APD⊥平面ABCD,AB∥CD,CD=AD=AP=4,AB=2,AD⊥AP,CB=2$\sqrt{5}$.
如图,已知平面APD⊥平面ABCD,AB∥CD,CD=AD=AP=4,AB=2,AD⊥AP,CB=2$\sqrt{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
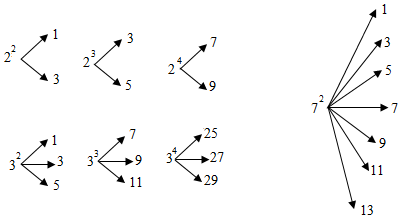 对于mn(m,n∈N且m,n≥2)可以按如下的方式进行“分解”,例如72的“分解“中最小的数是1,最大的数是13.若m3的“分解”中最小的数是111,则m=11.
对于mn(m,n∈N且m,n≥2)可以按如下的方式进行“分解”,例如72的“分解“中最小的数是1,最大的数是13.若m3的“分解”中最小的数是111,则m=11.查看答案和解析>>
科目:高中数学 来源:2015-2016学年江苏泰兴中学高二上学期期末数学(文)试卷(解析版) 题型:填空题
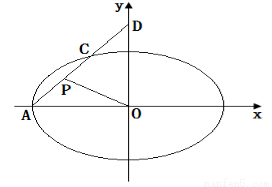
过椭圆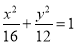 的左顶点
的左顶点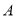 作斜率为
作斜率为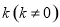 的直线
的直线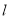 交椭圆于点
交椭圆于点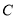 ,交
,交 轴于点
轴于点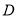 ,
,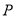 为
为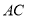 中点,定点
中点,定点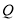 满足:对于任意的
满足:对于任意的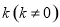 都有
都有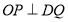 ,则
,则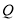 点的坐标为 .
点的坐标为 .
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,正方形ABCD的边长为$\sqrt{2}$,且对角线AC的中点为O,E为AD的中点,将△ADC沿对角线AC折起得平面ADC⊥平面ABC.
如图,正方形ABCD的边长为$\sqrt{2}$,且对角线AC的中点为O,E为AD的中点,将△ADC沿对角线AC折起得平面ADC⊥平面ABC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com