
在数列{an}中,a1=2,an+1=an+ln(1+ ),则an=( )
),则an=( )
(A)2+lnn(B)2+(n-1)lnn(C)2+nlnn(D)1+n+lnn
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十七第四章第三节练习卷(解析版) 题型:选择题
在△ABC中,∠C=90°,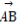 =(k,1),
=(k,1),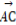 =(2,3),则k的值是( )
=(2,3),则k的值是( )
(A)5(B)-5(C) (D)-
(D)-
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十第五章第一节练习卷(解析版) 题型:解答题
在数列{an}中,a1=1,an+1=can+cn+1(2n+1)(n∈N*),其中实数c≠0.求{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十第五章第一节练习卷(解析版) 题型:填空题
设a1=2,an+1=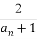 ,bn=|
,bn=|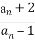 |,n∈N*,则数列{bn}的通项公式bn= .
|,n∈N*,则数列{bn}的通项公式bn= .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十四第五章第五节练习卷(解析版) 题型:解答题
已知某地今年年初拥有居民住房的总面积为a(单位:m2),其中有部分旧住房需要拆除.当地有关部门决定每年以当年年初住房面积的10%建设新住房,同时也拆除面积为b(单位:m2)的旧住房.
(1)分别写出第1年末和第2年末的实际住房面积的表达式.
(2)如果第5年末该地的住房面积正好比今年年初的住房面积增加了30%,则每年拆除的旧住房面积b是多少?(计算时取1.15=1.6)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十四第五章第五节练习卷(解析版) 题型:填空题
从盛满2升纯酒精的容器里倒出1升纯酒精,然后填满水,再倒出1升混合溶液后又用水填满,以此继续下去,则至少应倒 次后才能使纯酒精体积与总溶液的体积之比低于10%.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十六第六章第二节练习卷(解析版) 题型:选择题
对于实数x,当n≤x<n+1(n∈Z)时,规定[x]=n,则不等式4[x]2-36[x]+45<0的解集为( )
(A){x|2≤x<8} (B){x|2<x≤8}
(C){x|2≤x≤8} (D){x|2<x<8}
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十二第五章第三节练习卷(解析版) 题型:解答题
定义:若数列{An}满足An+1=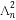 ,则称数列{An}为“平方递推数列”.已知数列{an}中,a1=2,点(an,an+1)在函数f(x)=2x2+2x的图象上,其中n为正整数.
,则称数列{An}为“平方递推数列”.已知数列{an}中,a1=2,点(an,an+1)在函数f(x)=2x2+2x的图象上,其中n为正整数.
(1)证明:数列{2an+1}是 “平方递推数列”,且数列{lg(2an+1)}为等比数列.
(2)设(1)中“平方递推数列”的前n项之积为Tn,即Tn=(2a1+1)(2a2+1)…(2an+1),求数列{an}的通项公式及Tn关于n的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com