
【题目】已知函数![]() ,若方程
,若方程![]() 有五个不同的根,则实数
有五个不同的根,则实数![]() 的取值范围为( )
的取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】分析:求出f(﹣x)的解析式,根据x的范围不同得出两个不同的方程,由两个方程的关系得出f(﹣x)=f(x)在(0,+∞)上有两解,根据函数图象和导数的几何意义得出a的范围.
详解:∵f(x)=![]() ,∴f(﹣x)=
,∴f(﹣x)=![]() .
.
显然x=0是方程f(﹣x)=f(x)的一个根,
当x>0时,ex=﹣ax,①
当x<0时,e﹣x=ax,②
显然,若x0为方程①的解,则﹣x0为方程②的解,
即方程①,②含有相同个数的解,
∵方程f(﹣x)=f(x)有五个不同的根,
∴方程①在(0,+∞)上有两解,
做出y=ex(x>0)和y=﹣ax(x>0)的函数图象,如图所示:

设y=kx与y=ex相切,切点为(x0,y0),
则 ,解得x0=1,k=e.
,解得x0=1,k=e.
∵y=ex与y=﹣ax在(0,+∞)上有两个交点,
∴﹣a>e,即a<﹣e.
故选: C.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:
【题目】如图,将一个各面都涂了油漆的正方体,切割为125个同样大小的小正方体,经过搅拌后,从中随机取一个小正方体,记它的涂漆面数为X,则X的均值E(X)=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 已知a1=1, ![]() ,n∈N* .
,n∈N* .
(1)求a2的值;
(2)求数列{an}的通项公式;
(3)证明:对一切正整数n,有 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列![]() 的前
的前![]() 项和为
项和为![]() ,对任意
,对任意![]() ,点
,点![]() 都在函数
都在函数 ![]() 的图象上.
的图象上.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)已知数列![]() 满足
满足![]() ,若对任意
,若对任意![]() ,存在
,存在![]() 使得
使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆Γ: ![]() =1(a>b>0)的左右焦点分别为F1 , F2 , 焦距为2c,若直线y=
=1(a>b>0)的左右焦点分别为F1 , F2 , 焦距为2c,若直线y= ![]() 与椭圆Γ的一个交点M满足∠MF1F2=2∠MF2F1 , 则该椭圆的离心率等于 .
与椭圆Γ的一个交点M满足∠MF1F2=2∠MF2F1 , 则该椭圆的离心率等于 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x|x2-3x+2=0},B={x|x2+(a-1)x+a2-5=0}.
(1)若A∩B={2},求实数a的值;
(2)若A∪B=A,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,以
中,以![]() 轴为始边做两个锐角
轴为始边做两个锐角![]() ,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为
,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为![]()
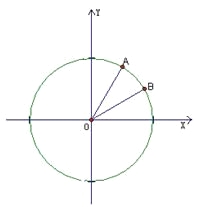
(1)求![]() 的值; (2)求
的值; (2)求![]() 的值。
的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
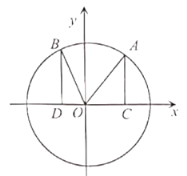
【题目】如图,在平面直角坐标系![]() 中,单位圆
中,单位圆![]() 上存在两点
上存在两点![]() ,满足
,满足![]() 均与
均与![]() 轴垂直,设
轴垂直,设![]() 与
与![]() 的面积之和记为
的面积之和记为![]() .
.
![]() 若
若![]() ,求
,求![]() 的值;
的值;
![]() 若对任意的
若对任意的![]() ,存在
,存在![]() ,使得
,使得![]() 成立,且实数
成立,且实数![]() 使得数列
使得数列![]() 为递增数列,其中
为递增数列,其中![]() 求实数
求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com