
【题目】如图,一楼房高![]() 为
为![]() 米,某广告公司在楼顶安装一块宽
米,某广告公司在楼顶安装一块宽![]() 为
为![]() 米的广告牌,
米的广告牌,![]() 为拉杆,广告牌的倾角为
为拉杆,广告牌的倾角为![]() ,安装过程中,一身高为
,安装过程中,一身高为![]() 米的监理人员
米的监理人员![]() 站在楼前观察该广传牌的安装效果:为保证安全,该监理人员不得站在广告牌的正下方:设
站在楼前观察该广传牌的安装效果:为保证安全,该监理人员不得站在广告牌的正下方:设![]() 米,该监理人员观察广告牌的视角
米,该监理人员观察广告牌的视角![]() .
.

(1)试将![]() 表示为
表示为![]() 的函数;
的函数;
(2)求点![]() 的位置,使
的位置,使![]() 取得最大值.
取得最大值.
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
【题目】有甲、乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩,得到如下所示的列联表:
优秀 | 非优秀 | 总计 | |
甲班 | 10 |
| |
乙班 |
| 30 | |
总计 |
|
已知在全部105人中随机抽取1人,成绩优秀的概率为![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
A. 列联表中![]() 的值为30,
的值为30,![]() 的值为35
的值为35
B. 列联表中![]() 的值为15,
的值为15,![]() 的值为50
的值为50
C. 根据列联表中的数据,若按![]() 的可靠性要求,能认为“成绩与班级有关系”
的可靠性要求,能认为“成绩与班级有关系”
D. 根据列联表中的数据,若按![]() 的可靠性要求,不能认为“成绩与班级有关系”
的可靠性要求,不能认为“成绩与班级有关系”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() 的圆心为
的圆心为![]() .已知点
.已知点![]() ,且
,且![]() 为圆
为圆![]() 上的动点,线段
上的动点,线段![]() 的中垂线交
的中垂线交![]() 于点
于点![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,若四边形
,若四边形![]() 的四个顶点都在曲线
的四个顶点都在曲线![]() 上,对角线
上,对角线![]() ,
,![]() 互相垂直并且它们的交点恰为点
互相垂直并且它们的交点恰为点![]() ,求四边形
,求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的方程为
的方程为![]() ,过点
,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为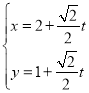 (
(![]() 为参数).
为参数).
(Ⅰ)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,求
两点,求![]() 的值,并求定点
的值,并求定点![]() 到
到![]() ,
,![]() 两点的距离之积.
两点的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“微信运动”是腾讯开发的一个记录跑步或行走情况(步数里程)的公众号用户通过该公众号可查看自己某时间段的运动情况.某人根据2018年1月至2018年11月期间每月离步的里程(单位:十公里)的数据绘制了下面的折线图.根据该折线图,下列结论正确的是( )

A.月跑步里程逐月增加
B.月跑步里程最大值出现在10月
C.月跑步里程的中位数为5月份对应的里程数
D.1月至5月的月跑步里程相对于6月至11月波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了选派学生参加“厦门市中学生知识竞赛”,某校对本校2000名学生进行选拔性测试,得到成绩的频率分布直方图(如图).规定:成绩大于或等于110分的学生有参赛资格,成绩110分以下(不包括110分)的学生则被淘汰.

(1)求获得参赛资格的学生人数;
(2)根据频率分布直方图,估算这2000名学生测试的平均成绩(同组中的数据用该组区间点值作代表);
(3)若知识竞赛分初赛和复赛,在初赛中有两种答题方案:
方案一:每人从5道备选题中任意抽出1道,若答对,则可参加复赛,否则被淘汰;
方案二:每人从5道备选题中任意抽出3道,若至少答对其中2道,则可参加复赛,否则被海汰.
已知学生甲只会5道备选题中的3道,那么甲选择哪种答题方案,进入复赛的可能性更大?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() ABC的三个顶点A(-3,0),B(2,1),C(-2,3).求:
ABC的三个顶点A(-3,0),B(2,1),C(-2,3).求:
(Ⅰ)BC边上中线AD所在直线的方程;
(Ⅱ)BC边上高线AH所在直线的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com