解:(1)∵数列{a
n}的首项a
1=2,公比q=

,∴
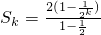
=
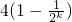
≥2,
而0<c<2,对任意的正整数k都有
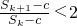
成立,∴S
k+1-c<2S
k-2c,化为c<2S
k-S
k+1,
把S
k,S
k+1代入计算得
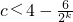
,
先研究函数g(x)=
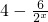
的单调性,x∈(0,+∞).
∵y=2
x在x∈(0,+∞)上单调递增,∴函数
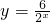
在x∈(0,+∞)上单调递减,
∴函数y=
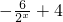
在x∈(0,+∞)上单调递增.
即g(k)=
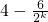
关于k单调递增,又对任意的k恒成立,∴当k=1时g(k)取得最小值,∴0<c<
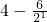
=1,即0<c<1.
(2)符号为负.
证明:当q=1时,S
nS
n+2-
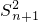
=
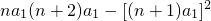
=
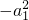
<0,
当q≠1时,∵{a
n}是由正数组成的数列,∴q>0.
当q>0时且q≠1时,S
nS
n+2-
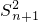
=
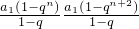
-
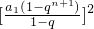
=
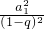
[(1-q
n)(1-q
n+2)-(1-q
n+1)
2]
=
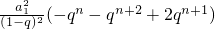
=

<0.
综上可知:S
nS
n+2-
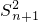
为负.
(3)假设存在一个正常数m满足题意,则有
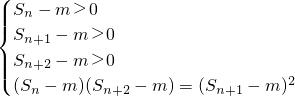
,
∴

=m(S
n+S
n+2-2S
n+1)(*),
∵S
n+S
n+2-2S
n+1=(S
n-m)+(S
n+2-m)-2(S
n+1-m)≥
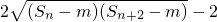
(S
n+1-m)=0,
∴S
n+S
n+2-2S
n+1≥0,
∴m(S
n+S
n+2-2S
n+1)≥0,
由(1)得S
nS
n+2-
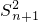
<0.
∴(*)式不成立.
故不存在正常数m使结论成立.
分析:(1)利用等比数列的前n项和公式及不等式的性质即可得出;
(2)通过对公比q分类讨论,利用等比数列的前n和公式即可得出;
(3)假设存在一个正常数m满足题意,利用已知条件就基本不等式的性质得出矛盾,从而可知不存在正常数m满足题意.
点评:熟练掌握等比数列的前n项和公式、对公比q分类讨论、不等式的性质、基本不等式的性质、对数的运算性质是解题的关键.

 时,对任意的正整数k都有
时,对任意的正整数k都有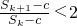 (0<c<2)成立,求c的取值范围;
(0<c<2)成立,求c的取值范围;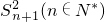 的符号,并加以证明;
的符号,并加以证明; ,∴
,∴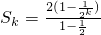 =
=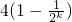 ≥2,
≥2,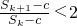 成立,∴Sk+1-c<2Sk-2c,化为c<2Sk-Sk+1,
成立,∴Sk+1-c<2Sk-2c,化为c<2Sk-Sk+1,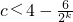 ,
,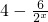 的单调性,x∈(0,+∞).
的单调性,x∈(0,+∞).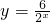 在x∈(0,+∞)上单调递减,
在x∈(0,+∞)上单调递减,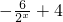 在x∈(0,+∞)上单调递增.
在x∈(0,+∞)上单调递增.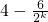 关于k单调递增,又对任意的k恒成立,∴当k=1时g(k)取得最小值,∴0<c<
关于k单调递增,又对任意的k恒成立,∴当k=1时g(k)取得最小值,∴0<c<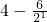 =1,即0<c<1.
=1,即0<c<1.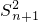 =
=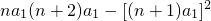 =
=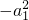 <0,
<0,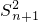 =
=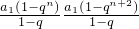 -
-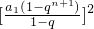
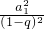 [(1-qn)(1-qn+2)-(1-qn+1)2]
[(1-qn)(1-qn+2)-(1-qn+1)2]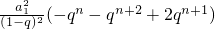
 <0.
<0.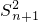 为负.
为负.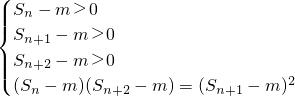 ,
, =m(Sn+Sn+2-2Sn+1)(*),
=m(Sn+Sn+2-2Sn+1)(*),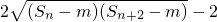 (Sn+1-m)=0,
(Sn+1-m)=0,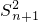 <0.
<0.
