
【题目】已知函数![]() .
.
(I) 当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(II) 当![]() 时,
时,![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ) 单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(Ⅱ)![]() .
.
【解析】试题分析:(Ⅰ)对函数![]() 求导,令
求导,令![]() ,由
,由![]() ,可得
,可得![]() 有两个不同解,结合函数
有两个不同解,结合函数![]() 的定义域,即可求得函数
的定义域,即可求得函数![]() 的单调区间;(Ⅱ)当
的单调区间;(Ⅱ)当![]() 时,
时,![]() 恒成立等价于当
恒成立等价于当![]() 时,
时,![]() 恒成立,令
恒成立,令![]() ,求导得
,求导得![]() ,设
,设![]() ,利用导数研究函数
,利用导数研究函数![]() 的单调性,从而可确定
的单调性,从而可确定![]() ,然后对
,然后对![]() 分类讨论,即可求得
分类讨论,即可求得![]() 的取值范围.
的取值范围.
试题解析:(Ⅰ)∵![]() ,函数定义域为:
,函数定义域为:![]()
∴![]()
令![]() ,由
,由![]() 可知,
可知,![]()
从而![]() 有两个不同解.
有两个不同解.
令![]() ,则
,则![]()
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以函数![]() 的单调递增区间为
的单调递增区间为![]() ,
,
单调递减区间为![]() .
.
(Ⅱ)由题意得,当![]() 时,
时,![]() 恒成立.
恒成立.
令![]() ,求导得
,求导得![]() ,
,
设![]() ,则
,则![]() ,
,
∵![]()
∴![]()
∴![]() ,
,
∴![]() 在
在![]() 上单调递增,即
上单调递增,即![]() 在
在![]() 上单调递增,
上单调递增,
∴![]()
①当![]() 时,
时,![]() ,
,
此时,![]() 在
在![]() 上单调递增,而
上单调递增,而![]() .
.
∴![]() 恒成立,满足题意.
恒成立,满足题意.
②当![]() 时,
时,![]() ,而
,而![]()
根据零点存在性定理可知,存在![]() ,使得
,使得![]() .
.
当![]() 时,
时,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
∴有![]() ,
,
∴![]() 恒成立矛盾
恒成立矛盾
∴实数![]() 的取值范围为
的取值范围为![]()


 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:
【题目】某地发生地质灾害,使当地的自来水受到了污染,某部门对水质检测后,决定往水中投放一种药剂来净化水质.已知每投放质量为m的药剂后,经过x天该药剂在水中释放的浓度y(毫克/升)满足![]() ,其中
,其中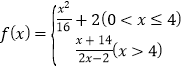 ,当药剂在水中释放的浓度不低于4(毫克/升)时称为有效净化;当药剂在水中释放的浓度不低于4(毫克/升)且不高于10(毫克/升)时称为最佳净化.
,当药剂在水中释放的浓度不低于4(毫克/升)时称为有效净化;当药剂在水中释放的浓度不低于4(毫克/升)且不高于10(毫克/升)时称为最佳净化.
(1)如果投放的药剂质量为m=4,试问自来水达到有效净化一共可持续几天?
(2)如果投放的药剂质量为m,为了使在7天(从投放药剂算起包括7天)之内的自来水达到最佳净化,试确定应该投放的药剂质量m的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在古代,直角三角形中较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.三国时期吴国数学家赵爽用“弦图”( 如图) 证明了勾股定理,证明方法叙述为:“按弦图,又可以勾股相乘为朱实二,倍之为朱实四,以勾股之差自相乘为中黄实,加差实,亦成弦实.”这里的“实”可以理解为面积.这个证明过程体现的是这样一个等量关系:“两条直角边的乘积是两个全等直角三角形的面积的和(朱实二 ),4个全等的直角三角形的面积的和(朱实四) 加上中间小正方形的面积(黄实) 等于大正方形的面积(弦实)”. 若弦图中“弦实”为16,“朱实一”为![]() ,现随机向弦图内投入一粒黄豆(大小忽略不计),则其落入小正方形内的概率为( )
,现随机向弦图内投入一粒黄豆(大小忽略不计),则其落入小正方形内的概率为( )
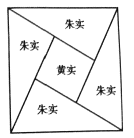
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ).
).
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)若函数![]() 的图象在点
的图象在点![]() 处的切线的倾斜角为
处的切线的倾斜角为![]() ,且函数
,且函数![]() (
(![]() )当且仅当在
)当且仅当在![]() 处取得极值,其中
处取得极值,其中![]() 为
为![]() 的导函数,求
的导函数,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】元旦晚会期间,高三二班的学生准备了6 个参赛节目,其中有 2 个舞蹈节目,2 个小品节目,2个歌曲节目,要求歌曲节目一定排在首尾,另外2个舞蹈节目一定要排在一起,则这 6 个节目的不同编排种数为
A. 48 B. 36 C. 24 D. 12
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线顶点在原点,焦点在x轴上,且过点(4,4),焦点为F.
(1)求抛物线的焦点坐标和标准方程;
(2)P是抛物线上一动点,M是PF的中点,求M的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以原点
),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() 是曲线
是曲线![]() 上一点,若点
上一点,若点![]() 到曲线
到曲线![]() 的最小距离为
的最小距离为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人参加普法知识竞赛,共有5题,选择题3个,判断题2个,甲、乙两人各抽一题.
(1)甲、乙两人中有一个抽到选择题,另一个抽到判断题的概率是多少?
(2)甲、乙两人中至少有一人抽到选择题的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com