
【题目】某地区有3个不同值班地点,每个值班地点需配一名医务人员和两名警察,现将3名医务人员(1男2女)和6名警察(4男2女)分配到这3个地点去值班,要求每个值班地点至少有一名女性,则共有______种不同分配方案.(用具体数字作答)
科目:高中数学 来源: 题型:
【题目】近年,国家逐步推行全新的高考制度.新高考不再分文理科,某省采用3+3模式,其中语文、数学、外语三科为必考科目,满分各150分,另外考生还要依据想考取的高校及专业的要求,结合自己的兴趣爱好等因素,在思想政治、历史、地理、物理、化学、生物6门科目中自选3门参加考试(6选3),每科目满分100分.为了应对新高考,某高中从高一年级1000名学生(其中男生550人,女生450人)中,采用分层抽样的方法从中抽取![]() 名学生进行调查.
名学生进行调查.
(1)已知抽取的![]() 名学生中含男生55人,求
名学生中含男生55人,求![]() 的值;
的值;
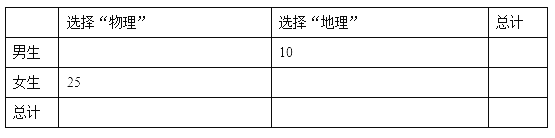
(2)学校计划在高一上学期开设选修中的“物理”和“地理”两个科目,为了了解学生对这两个科目的选课情况,对在(1)的条件下抽取到的![]() 名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目),下表是根据调查结果得到的
名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目),下表是根据调查结果得到的![]() 列联表. 请将列联表补充完整,并判断是否有 99%的把握认为选择科目与性别有关?说明你的理由;
列联表. 请将列联表补充完整,并判断是否有 99%的把握认为选择科目与性别有关?说明你的理由;
(3)在抽取到的女生中按(2)中的选课情况进行分层抽样,从中抽出9名女生,再从这9名女生中抽取4人,设这4人中选择“地理”的人数为![]() ,求
,求![]() 的分布列及期望.
的分布列及期望.
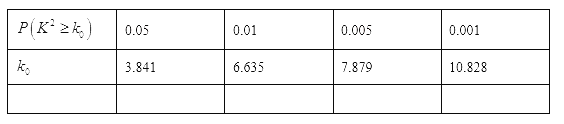
附:![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】手机运动计步已成为一种时尚,某中学统计了该校教职工一天行走步数(单位:百步),绘制出如下频率分布直方图:
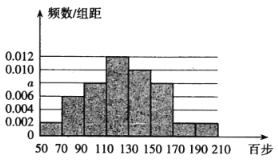
(Ⅰ)求直方图中![]() 的值,并由频率分布直方图估计该校教职工一天步行数的中位数;
的值,并由频率分布直方图估计该校教职工一天步行数的中位数;
(Ⅱ)若该校有教职工175人,试估计一天行走步数不大于130百步的人数;
(Ⅲ)在(Ⅱ)的条件下该校从行走步数大于150百步的3组教职工中用分层抽样的方法选取6人参加远足活动,再从6人中选取2人担任领队,求这两人均来自区间![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,![]() ,
,![]() 是
是![]() 轴上关于原点
轴上关于原点![]() 对称的两定点,点
对称的两定点,点![]() 满足
满足![]() ,点
,点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求![]() 的方程;
的方程;
(2)过![]() 的直线与
的直线与![]() 交于点
交于点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,
,![]() 的中垂线分别与
的中垂线分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() ,问
,问![]() 是否成立?若成立,求出直线
是否成立?若成立,求出直线![]() 的方程;若不成立,请说明理由.
的方程;若不成立,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某两名高三学生在连续9次数学测试中的成绩(单位:分)进行统计得到折线图,下面是关于这两位同学的数学成绩分析.
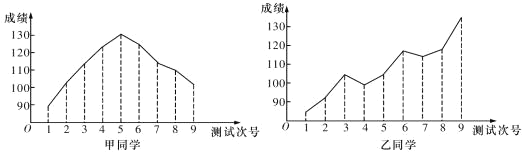
①甲同学的成绩折线图具有较好的对称性,故平均成绩为130分;
②根据甲同学成绩折线图提供的数据进行统计,估计该同学平均成绩在区间![]() 内;
内;
③乙同学的数学成绩与测试次号具有比较明显的线性相关性,且为正相关;
④乙同学连续九次测验成绩每一次均有明显进步.
其中正确的个数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线![]() 的参数方程为
的参数方程为![]() (t为参数,
(t为参数,![]() ).在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线
).在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 和
和![]() 的普通方程;
的普通方程;
(2)若直线l的极坐标方程为![]() ,其中
,其中![]() 满足
满足![]() ,若曲线
,若曲线![]() 和
和![]() 的公共点均在l上,求
的公共点均在l上,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊数学家阿波罗尼奥斯发现:平面上到两定点![]() ,
,![]() 距离之比为常数
距离之比为常数![]() 且
且![]() 的点的轨迹是一个圆心在直线
的点的轨迹是一个圆心在直线![]() 上的圆,该圆简称为阿氏圆.根据以上信息,解决下面的问题:如图,在长方体
上的圆,该圆简称为阿氏圆.根据以上信息,解决下面的问题:如图,在长方体![]() 中,
中,![]() ,点
,点![]() 在棱
在棱![]() 上,
上,![]() ,动点
,动点![]() 满足
满足![]() .若点
.若点![]() 在平面
在平面![]() 内运动,则点
内运动,则点![]() 所形成的阿氏圆的半径为________;若点
所形成的阿氏圆的半径为________;若点![]() 在长方体
在长方体![]() 内部运动,
内部运动,![]() 为棱
为棱![]() 的中点,
的中点,![]() 为
为![]() 的中点,则三棱锥
的中点,则三棱锥![]() 的体积的最小值为___________.
的体积的最小值为___________.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com