
【题目】已知命题p:![]() ,
,![]() ;命题q:方程
;命题q:方程![]() 表示双曲线.
表示双曲线.
⑴若命题p为真命题,求实数m的取值范围;
⑵若命题“![]() ”为真命题,“
”为真命题,“![]() ”为假命题,求实数m的取值范围.
”为假命题,求实数m的取值范围.
科目:高中数学 来源: 题型:
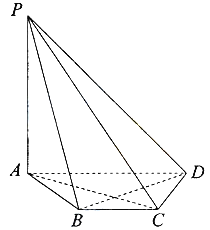
【题目】如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是等腰梯形,AD∥BC,AC⊥BD.
(Ⅰ)证明:BD⊥PC;
(Ⅱ)若AD=4,BC=2,直线PD与平面PAC所成的角为30°,求四棱锥P-ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学团委组织了“纪念抗日战争胜利73周年”的知识竞赛,从参加竞赛的学生中抽出60名学生,将其成绩(均为整数)分成六段![]() ,
,![]() ,…,
,…,![]() 后,画出如图所示的部分频率分布直方图.观察图形给出的信息,回答下列问题:
后,画出如图所示的部分频率分布直方图.观察图形给出的信息,回答下列问题:
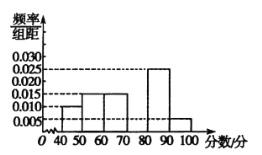
(1)求第四组的频率,并补全这个频率分布直方图;
(2)估计这次竞赛的及格率(60分及以上为及格)和平均分(同一组中的数据用该组区间的中点值代表)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】朱世杰是元代著名数学家,他所著《算学启蒙》是一部在中国乃至世界最早的科学普及著作.《算学启蒙》中提到一些堆垛问题,如“三角垛果子”,就是将一样大小的果子堆垛成正三棱锥,每层皆堆成正三角形,从上向下数,每层果子数分别为1,3,6,10,…,现有一个“三角垛果子”,其最底层每边果子数为10,则该层果子数为( )
A. 50B. 55C. 100D. 110
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,且PA=PD=![]() AD,E,F分别为PC,BD的中点.
AD,E,F分别为PC,BD的中点.

求证:(1)EF∥平面PAD;
(2)PA⊥平面PDC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某音乐院校举行“校园之星”评选活动,评委由本校全体学生组成,对![]() 两位选手,随机调查了
两位选手,随机调查了![]() 个学生的评分,得到下面的茎叶图:
个学生的评分,得到下面的茎叶图:
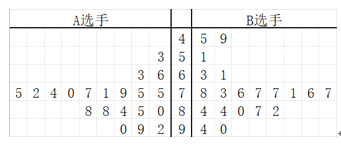
![]() 通过茎叶图比较
通过茎叶图比较![]() 两位选手所得分数的平均值及分散程度(不要求计算出具体值,得出结论即可);
两位选手所得分数的平均值及分散程度(不要求计算出具体值,得出结论即可);
![]() 校方将会根据评分记过对参赛选手进行三向分流:
校方将会根据评分记过对参赛选手进行三向分流:
所得分数 | 低于 |
| 不低于 |
分流方向 | 淘汰出局 | 复赛待选 | 直接晋级 |
记事件![]() “
“![]() 获得的分流等级高于
获得的分流等级高于![]() ”,根据所给数据,以事件发生的频率作为相应事件发生的概率,求事件
”,根据所给数据,以事件发生的频率作为相应事件发生的概率,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两个学校高三年级分别有1100人,1000人,为了了解两个学校全体高三年级学生在该地区一模考试的数学成绩情况,采用分层抽样方法从两个学校一共抽取了105名学生的数学成绩,并作出了频数分布统计表如下:

(1)计算![]() ,
,![]() 的值;
的值;
(2)若规定考试成绩在![]() 为优秀,请根据样本估计乙校数学成绩的优秀率;
为优秀,请根据样本估计乙校数学成绩的优秀率;
(3)若规定考试成绩在![]() 内为优秀,由以上统计数据填写下面
内为优秀,由以上统计数据填写下面![]() 列联表,若按是否优秀来判断,是否有
列联表,若按是否优秀来判断,是否有![]() 的把握认为两个学校的数学成绩有差异.
的把握认为两个学校的数学成绩有差异.

附: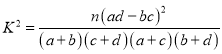 ,
,![]() .
.
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了弘扬中华民族传统文化,某中学高二年级举行了“爱我中华,传诵经典”的考试,并从中随机抽取了![]() 名学生的成绩(满分
名学生的成绩(满分![]() 分)作为样本,其中成绩不低于
分)作为样本,其中成绩不低于![]() 分的学生被评为优秀生,得到成绩分布的频率分布直方图如图所示.
分的学生被评为优秀生,得到成绩分布的频率分布直方图如图所示.
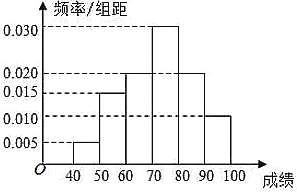
(1)若该年级共有![]() 名学生,试利用样本估计该年级这次考试中优秀生人数;
名学生,试利用样本估计该年级这次考试中优秀生人数;
(2)试估计这次参加考试的学生的平均成绩(同一组数据用该组区间中点值作代表);
(3)若在样本中,利用分层抽样从成绩不低于![]() 分的学生中随机抽取
分的学生中随机抽取![]() 人,再从中抽取
人,再从中抽取![]() 人赠送一套国学经典典籍,试求恰好抽中
人赠送一套国学经典典籍,试求恰好抽中![]() 名优秀生的概率.
名优秀生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com