
| A. | -2009 | B. | -3010 | C. | -3014 | D. | 3028 |
分析 通过写出前几项的值可知满足条件的数列{an}的通项公式,进而利用分组法求和计算即得结论.
解答 解:依题意,要使其前2009项的和S2009的最小值只需每一项的值都取最小值即可,
∵a1=2,绝对公和d=3,
∴a2=-1或a2=1(舍),
∴a3=-2或a3=2(舍),
∴a4=-1或a4=1(舍),
…
∴满足条件的数列{an}的通项公式an=$\left\{\begin{array}{l}{2,}&{n=1}\\{-2,}&{n为大于1的奇数}\\{-1,}&{n为偶数}\end{array}\right.$,
∴所求值为a1+(a2+a3)+(a4+a5)+…+(a2008+a2009)
=2+(-1-2)×$\frac{2009-1}{2}$
=-3010,
故选:B.
点评 本题考查考查数列的求和,找出满足条件的数列的通项公式是解决本题的关键,注意解题方法的积累,属于中档题.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
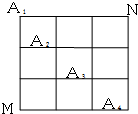 如图,在某城市中,M,N两地之间有整齐的方格形道路网,A1、A2、A3、A4是道路网中位于一条对角线上的4个交汇处,今甲由道路网M处出发随机地选择一条沿街的最短路径到达N处.
如图,在某城市中,M,N两地之间有整齐的方格形道路网,A1、A2、A3、A4是道路网中位于一条对角线上的4个交汇处,今甲由道路网M处出发随机地选择一条沿街的最短路径到达N处.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 随机数组的特征 | 3个数字均相同 | 恰有2个数字相同 | 其余情况 |
| 奖金(单位:元) | 500 | 200 | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有最大值,无最小值 | B. | 有最大值和最小值 | ||
| C. | 有最小值,无最大值 | D. | 无最值 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
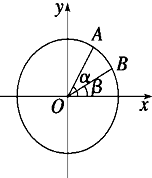 如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α、β,它们的终边分别与单位圆相交于A、B两点.已知A、B的横坐标分别为x1,x2.
如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α、β,它们的终边分别与单位圆相交于A、B两点.已知A、B的横坐标分别为x1,x2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com