
【题目】已知函数f(x)=aex﹣blnx,曲线y=f(x)在点(1,f(1))处的切线方程为 ![]() .
.
(1)求a,b;
(2)证明:f(x)>0.
【答案】
(1)解:函数f(x)=aex﹣blnx,
求导函数可得f′(x)=aex﹣ ![]() (x>0)
(x>0)
∵曲线y=f(x)在(1,f(1))处的切线方程为 ![]() ,
,
∴f(1)= ![]() ,f′(1)=
,f′(1)= ![]() ﹣1,
﹣1,
∴ae= ![]() ,ae﹣b=
,ae﹣b= ![]() ﹣1,
﹣1,
∴a= ![]() ,b=1;
,b=1;
(2)证明:函数f(x)=ex﹣2﹣lnx,
由y=ex﹣2﹣(x﹣1)的导数y′=ex﹣2﹣1,
当x>2时,导数y′>0,函数y递增;
当x<2时,导数y′<0,函数y递减.
可得函数y在x=2处取得极小值也为最小值0,
即有ex﹣2≥x﹣1;
由y=lnx﹣(x﹣1)的导数为y′= ![]() ﹣1,
﹣1,
当x>1时,导数y′<0,函数y递减;
当0<x<1时,导数y′>0,函数y递增.
可得函数y在x=1处取得极大值也为最大值0,
即有lnx≤x﹣1;
由于等号不同时取得,
则ex﹣2>lnx,
即有f(x)>0成立
【解析】(1)求导函数,利用曲线y=f(x)在(1,f(1))处的切线方程,可得f(1)= ![]() ,f′(1)=
,f′(1)= ![]() ﹣1,由此可求a,b的值;(2)构造函数y=ex﹣2﹣(x﹣1),求导函数,确定函数的单调区间,从而可得函数的最小值;构造y=lnx﹣(x﹣1),求出导数和单调区间,可得最大值,故可得证.
﹣1,由此可求a,b的值;(2)构造函数y=ex﹣2﹣(x﹣1),求导函数,确定函数的单调区间,从而可得函数的最小值;构造y=lnx﹣(x﹣1),求出导数和单调区间,可得最大值,故可得证.
【考点精析】掌握利用导数研究函数的单调性是解答本题的根本,需要知道一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


科目:高中数学 来源: 题型:
【题目】某地电影院为了了解当地影迷对快要上映的一部电影的票价的看法,进行了一次调研,得到了票价x(单位:元)与渴望观影人数y(单位:万人)的结果如下表:
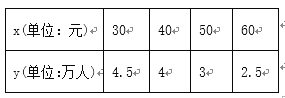
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程;
(2)根据(1)中求出的线性回归方程,若票价定为70元,预测该电影院渴望观影人数.附:回归直线的斜率和截距的最小二乘法估计公式分别为: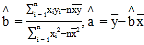
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=2 ![]() ,AD=
,AD= ![]() ,M为DC的中点,将△DAM沿AM折到△D′AM的位置,AD′⊥BM.
,M为DC的中点,将△DAM沿AM折到△D′AM的位置,AD′⊥BM. 
(1)求证:平面D′AM⊥平面ABCM;
(2)若E为D′B的中点,求二面角E﹣AM﹣D′的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,其中b≠c,且bcosB=ccosC,延长线段BC到点D,使得BC=4CD=4,∠CAD=30°, 
(Ⅰ)求证:∠BAC是直角;
(Ⅱ)求tan∠D的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知随圆E: ![]() +
+ ![]() =1(a>b>0)与过原点的直线交于A、B两点,右焦点为F,∠AFB=120°,若△AFB的面积为4
=1(a>b>0)与过原点的直线交于A、B两点,右焦点为F,∠AFB=120°,若△AFB的面积为4 ![]() ,则椭圆E的焦距的取值范围是( )
,则椭圆E的焦距的取值范围是( )
A.[2,+∞)
B.[4,+∞)
C.[2 ![]() ,+∞)
,+∞)
D.[4 ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】方程为x2+y2﹣4x﹣2y+4=0.以O为极点,x轴正半轴为极轴建立极坐标系.
(1)求l的普通方程与C的极坐标方程;
(2)已知l与C交于P,Q,求|PQ|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() =(sinx,cos2x),
=(sinx,cos2x), ![]() =(
=( ![]() cosx,1),x∈R,设f(x)=
cosx,1),x∈R,设f(x)= ![]()
![]() .
.
(1)求f(x)的解析式及单调递增区间;
(2)在△ABC中,角A,B,C所对的边分别为a,b,c,且a=2,f(A)=1,求△ABC面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com