
【题目】函数y=Asin(ωx+φ)在一个周期内的图象如图,此函数的解析式为( ) 
A.y=2sin(2x+ ![]() )
)
B.y=2sin(2x+ ![]() )??
)??
C.y=2sin( ![]() ﹣
﹣ ![]() )
)
D.y=2sin(2x﹣ ![]() )
)
科目:高中数学 来源: 题型:
【题目】如图,某城市有一块半径为40m的半圆形(以O为圆心,AB为直径)绿化区域,现计划对其进行改建.在AB的延长线上取点D,使OD=80m,在半圆上选定一点C,改建后的绿化区域由扇形区域AOC和三角形区域COD组成,其面积为S m2. 设∠AOC=x rad.
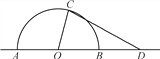
(1)写出S关于x的函数关系式S(x),并指出x的取值范围;
(2)张强同学说:当∠AOC=![]() 时,改建后的绿化区域面积S最大.张强同学的说法正确吗?若不正确,请求出改建后的绿化区域面积S最大值.
时,改建后的绿化区域面积S最大.张强同学的说法正确吗?若不正确,请求出改建后的绿化区域面积S最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先阅读下列结论的证法,再解决后面的问题:已知a1 , a2∈R,a1+a2=1,求证a12+a22≥ ![]() .
.
【证明】构造函数f(x)=(x﹣a1)2+(x﹣a2)2
则f(x)=2x2﹣2(a1+a2)x+a12+a22
=2x2﹣2x+a12+a22
因为对一切x∈R,恒有f(x)≥0.
所以△=4﹣8(a12+a22)≤0,从而得a12+a22≥ ![]() ,
,
(1)若a1 , a2 , …,an∈R,a1+a2+…+an=1,请写出上述结论的推广式;
(2)参考上述解法,对你推广的结论加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的部分图象如图所示.
)的部分图象如图所示. 
(1)求函数的解析式;
(2)设 ![]() π<x<
π<x< ![]() π,且方程f(x)=m有两个不同的实数根,求实数m的取值范围和这两个根的和.
π,且方程f(x)=m有两个不同的实数根,求实数m的取值范围和这两个根的和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知y=f(x)是R上的可导函数,对于任意的正实数t,都有函数g(x)=f(x+t)﹣f(x)在其定义域内为减函数,则函数y=f(x)的图象可能为如图中( )
A.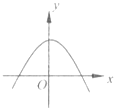
B.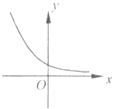
C.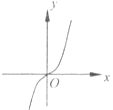
D.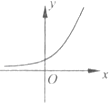
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com