
 如图,四棱锥P-ABCD的底面是边长为2的菱形,∠BAD=60°,△PAD是等边三角形,且$PB=\sqrt{6}$,M是棱PC上除P、C的任意一点,且$\frac{PM}{PC}=λ$
如图,四棱锥P-ABCD的底面是边长为2的菱形,∠BAD=60°,△PAD是等边三角形,且$PB=\sqrt{6}$,M是棱PC上除P、C的任意一点,且$\frac{PM}{PC}=λ$分析 (1)取AD中点为O,连结PO、BO、连BD与OC交于Q点,由题意知PO⊥AD,且$PO=\sqrt{3}$,再由已知可得$BO=\sqrt{3}$,在△POB中,利用勾股定理可得PO⊥BO,由线面垂直的判断得PO⊥平面ABCD,连结MQ,再由平行线截线段成比例定理可得,$λ=\frac{1}{3}$时,$\frac{OQ}{QC}=\frac{PM}{MC}$,从而得到PO∥MQ,再由面面垂直的判定得答案;
(2)当$λ=\frac{1}{2}$时,M是PC的中点,P到平面ABCD距离是M到平面BDC的距离的2倍,结合SABCD=2S△BCD,可得
VP-ABCD=4VM-BDC,由此得到两部分体积之比.
解答 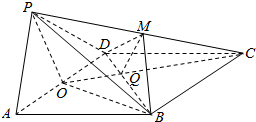 (1)证明:设AD中点为O,连结PO、BO、连BD与OC交于Q点,则PO⊥AD,且$PO=\sqrt{3}$,
(1)证明:设AD中点为O,连结PO、BO、连BD与OC交于Q点,则PO⊥AD,且$PO=\sqrt{3}$,
由已知,△ABD为等边三角形,∴$BO=\sqrt{3}$,在△POB中,
∵$PO=BO=\sqrt{3}$,PB=$\sqrt{6}$,
∴PO2+BO2=PB2,
∴PO⊥BO,则PO⊥平面ABCD,连结MQ,
∵OD∥BC,∴△BQC∽△OQD,则$\frac{OQ}{QC}=\frac{OD}{BC}=\frac{1}{2}$,
当$λ=\frac{1}{3}$时,$\frac{PM}{MC}=\frac{1}{2}$,
∴$\frac{OQ}{QC}=\frac{PM}{MC}$,则PO∥MQ,
∴MQ⊥平面ABCD,又MQ?平面BDM,
∴平面BDM⊥平面ABCD;
(2)解:当$λ=\frac{1}{2}$时,M是PC的中点,P到平面ABCD距离是M到平面BDC的距离的2倍,
又SABCD=2S△BCD,∴VP-ABCD=4VM-BDC,
则平面BDM将四棱锥分成的上下两部分体积为3:1.
点评 本题考查直线与平面平行的判断,考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力,是中档题.


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{OP}$=$\overrightarrow{OA}$+λ$\overrightarrow{OB}$ | B. | $\overrightarrow{OP}$=λ$\overrightarrow{OA}$+(1-λ)$\overrightarrow{OB}$ | ||
| C. | $\overrightarrow{OP}$=$\frac{1}{λ}$$\overrightarrow{OA}$+$\frac{1}{1+λ}$$\overrightarrow{OB}$ | D. | $\overrightarrow{OP}$=$\frac{1}{1+λ}$$\overrightarrow{OA}$+$\frac{λ}{1+λ}$$\overrightarrow{OB}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在如图所示的多面体PMBCA中,平面PAC⊥平面ABC,△PAC是边长为2的正三角形,PM∥BC,且BC=4,$AB=2\sqrt{5}$.
在如图所示的多面体PMBCA中,平面PAC⊥平面ABC,△PAC是边长为2的正三角形,PM∥BC,且BC=4,$AB=2\sqrt{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是②④(写出所有正确命题的编号).
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是②④(写出所有正确命题的编号).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com