练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    一批产品需要进行质量检验，检验方案是：先从这批产品中任取4件作检验，这4件产品中优质品的件数记为n.如果n＝3，再从这批产品中任取4件作检验，若都为优质品，则这批产品通过检验；如果n＝4，再从这批产品中任取1件作检验，若为优质品，则这批产品通过检验；其他情况下，这批产品都不能通过检验．
    假设这批产品的优质品率为50%，即取出的产品是优质品的概率都为，且各件产品是否为优质品相互独立．
    (1)求这批产品通过检验的概率；
    (2)已知每件产品检验费用为100元，凡抽取的每件产品都需要检验，对这批产品作质量检验所需的费用记为X(单位：元)，求X的分布列及数学期望．

    （1）（2）506.25

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    前不久，社科院发布了2013年度“全国城市居民幸福排行榜”，北京市成为本年度最“幸福城”.随后，某师大附中学生会组织部分同学，用“10分制”随机调查“阳光”社区人们的幸福度.现从调查人群中随机抽取16名，如图所示的茎叶图记录了他们的幸福度分数（以小数点前的一位数字为茎，小数点后一位为叶）：
    指出这组数据的众数和中位数；
    若幸福度不低于9.5分，则称该人的幸福度为“极幸福”.求从这16人中随机选取3人，至多有1人是“极幸福”的概率；
    以这16人的样本数据来估计整个社区的总体数据，若从该社区（人数很多）人选3人，记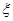表示抽到“极幸福”的人数，求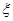的分布列及数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    甲、乙两名运动员参加“选拔测试赛”，在相同条件下，两人5次测试的成绩（单位：分）记录如下：
    甲  86   77   92   72   78
    乙  78   82   88   82   95
    （1）用茎叶图表示这两组数据；．
    （2）现要从中选派一名运动员参加比赛，你认为选派谁参赛更好？说明理由（不用计算）；
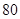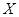    （3）若将频率视为概率，对运动员甲在今后三次测试成绩进行预测，记这三次成绩高于分的次数为，求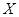的分布列和数学期望..

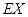    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    低碳生活，从“衣食住行”开始．在国内一些网站中出现了“碳足迹”的应用，人们可以由此计算出自己每天的碳排放量，如家居用电的二氧化碳排放量（千克）＝耗电度数，家用天然气的二氧化碳排放量（千克）＝天然气使用立方数等．某校开展“节能减排，保护环境，从我做起！”的活动，该校高一、六班同学利用假期在东城、西城两个小区进行了逐户的关于“生活习惯是否符合低碳排放标准”的调查．生活习惯符合低碳观念的称为“低碳家庭”，否则称为“非低碳家庭”．经统计，这两类家庭占各自小区总户数的比例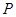数据如下：

    （1）如果在东城、西城两个小区内各随机选择2个家庭，求这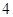个家庭中恰好有两个家庭是“低碳家庭”的概率；
    （2）该班同学在东城小区经过大力宣传节能减排的重要意义，每周“非低碳家庭”中有的家庭能加入到“低碳家庭”的行列中．宣传两周后随机地从东城小区中任选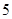个家庭，记表示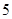个家庭中“低碳家庭”的个数，求和．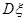

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    甲、乙两支排球队进行比赛，约定先胜3局者获得比赛的胜利，比赛随即结束，除第五局甲队获胜的概率是外，其余每局比赛甲队获胜的概率都是，假设各局比赛结果相互独立．
    (1)分别求甲队以3∶0，3∶1，3∶2胜利的概率；
    (2)若比赛结果为3∶0或3∶1，则胜利方得3分，对方得0分；若比赛结果为3∶2，则胜利方得2分、对方得1分．求乙队得分X的分布列．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    爸爸和亮亮用4张扑克牌(方块2，黑桃4，黑桃5，梅花5)玩游戏，他俩将扑克牌洗匀后，背面朝上放置在桌面上，爸爸先抽，亮亮后抽，抽出的牌不放回．

    (1)若爸爸恰好抽到了黑桃4．
    ①请把右面这种情况的树形图绘制完整；
    ②求亮亮抽出的牌的牌面数字比4大的概率．
    (11)爸爸、亮亮约定，若爸爸抽到的牌的牌面数字比亮亮的大，则爸爸胜；反之，则亮亮赢，你认为这个游戏是否公平?如果公平，请说明理由，如果不公平，更换一张扑克牌使游戏公平．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    一个袋中装有形状大小完全相同的球9个，其中红球3个，白球6个，每次随机取1个，直到取出3次红球即停止．
    (1)从袋中不放回地取球，求恰好取4次停止的概率P1；
    (2)从袋中有放回地取球．
    ①求恰好取5次停止的概率P2；
    ②记5次之内(含5次)取到红球的个数为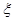，求随机变量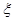的分布列及数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知一个矩形由三个相同的小矩形拼凑而成(如图所示)，用三种不同颜色给3个小矩形涂色，每个小矩形只涂一种颜色，求：

    （1）3个矩形都涂同一颜色的概率；
    （2）3个小矩形颜色都不同的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某联欢晚会举行抽奖活动，举办方设置了甲、乙两种抽奖方案，方案甲的中奖率为，中奖可以获得2分；方案乙的中奖率为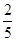，中奖可以得3分；未中奖则不得分．每人有且只有一次抽奖机会，每次抽奖中奖与否互不影响，晚会结束后凭分数兑换奖品．若小明选择方案甲抽奖，小红选择方案乙抽奖，记他们的累计得分为X，求X≤3的概率．

    查看答案和解析>>

    同步练习册答案