
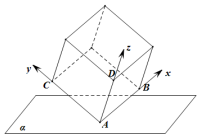
 如图,棱长为3的正方体的顶点A在平面α上,三条棱AB、AC、AD都在平面α的同侧.若顶点B,C到平面α的距离分别为1,$\sqrt{2}$.建立如图所示的空间直角坐标系,设平面α的一个法向量为(x1,y1,z1),顶点D到平面α的距离为h.若x1=1,则y1+z1+h=$\sqrt{2}$+2$\sqrt{6}$.
如图,棱长为3的正方体的顶点A在平面α上,三条棱AB、AC、AD都在平面α的同侧.若顶点B,C到平面α的距离分别为1,$\sqrt{2}$.建立如图所示的空间直角坐标系,设平面α的一个法向量为(x1,y1,z1),顶点D到平面α的距离为h.若x1=1,则y1+z1+h=$\sqrt{2}$+2$\sqrt{6}$. 分析 在正方体的8个顶点中,有关系的只有4个(其他顶点可不予理会),这4点组成直角四面体,这是解题的关键,
所以最终归结为:已知直角四面体的3个顶点A,B,C到平面α的距离依次为0,1,$\sqrt{2}$由此求出顶点D到平面α的距离和平面α的法向量.
解答 解:如图所示,
连结BC、CD、BD,则四面体A-BCD为直角四面体;
作平面α的法线AH,作BB1⊥平面α于B1,CC1⊥平面α于C1,DD1⊥平面α于D1;
连结AB1,AC1,AD1,令AH=h,DA=a,DB=b,DC=c,
由等体积可得$\frac{1}{{h}^{2}}$=$\frac{1}{{a}^{2}}+\frac{1}{{b}^{2}}+\frac{1}{{c}^{2}}$,
令∠BAB1=α,∠CAC1=γ,∠DAD1=β,
可得sin2α+sin2β+sin2γ=1,
设DD1=m,∵BB1=1,CC1=$\sqrt{2}$
∴$(\frac{1}{3})^{2}+(\frac{\sqrt{2}}{3})^{2}+(\frac{m}{3})^{2}$=1,
解得m=$\sqrt{6}$;即所求点D到平面α的距离为$\sqrt{6}$.
又α的法向量为$\overrightarrow{n}$=(x1,y1,z1)=(hcos($\frac{π}{2}$-α),hcos($\frac{π}{2}$-γ),hcos($\frac{π}{2}$-β))=(hsinα,hsinγ,hsinβ),
由hsinα=1,得hsinγ=$\sqrt{2}$,hsinβ=$\sqrt{6}$
∴$\overrightarrow{n}$=(1,$\sqrt{2}$,$\sqrt{6}$).
∴y1+z1+h=$\sqrt{2}$+2$\sqrt{6}$.
故答案为$\sqrt{2}$+2$\sqrt{6}$.
点评 本题主要考查了点、线、面间的距离计算,考查空间想象能力、运算能力和推理论证能力,属于创新题,难度大.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,4] | B. | (1,4) | C. | [4,5) | D. | (4,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 729 | B. | 665 | C. | 728 | D. | 636 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$-3 | B. | $\sqrt{5}$-2 | C. | 3-$\sqrt{5}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com