
已知数列![]() 的首项
的首项![]() 前
前![]() 项和为
项和为![]() ,且
,且![]()
(I)证明数列![]() 是等比数列;
是等比数列;
(II)令![]() ,求函数
,求函数![]() 在点
在点![]() 处的导数
处的导数![]() 并比较
并比较![]() 与
与![]() 的大小.
的大小.
解:(Ⅰ)由已知![]()
∴![]() 时,
时,![]()
两式相减,得![]() ,
,
即![]() ,从而
,从而![]() ,
,
当![]() 时
时![]()
∴![]()
又![]() ,∴
,∴![]() ,从而
,从而 ![]()
故总有![]() 、
、
又∵![]() ∴
∴![]() 从而
从而![]()
即![]() 是以
是以![]() 为首项,2为公比的等比数列。
为首项,2为公比的等比数列。
(II)由(I)知![]() 。
。
∵![]()
∴![]() 。
。
从而 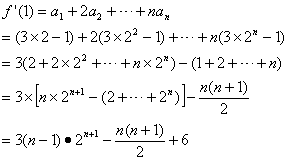
由上 ![]()
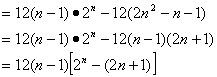 (*)
(*)
当![]() 时,(*)式=0 ∴
时,(*)式=0 ∴![]() ;
;
当![]() 时,(*)式=-12
时,(*)式=-12![]() ∴
∴![]()
当![]() 时,
时, ![]()
又![]()
∴![]()
即(*)![]()
从而![]()
(或用数学归纳法:n≥3时,猜想 ![]()
由于n-1>0,只要证明2n>2n+1。事实上,
1* 当 n=3时,23>2×3+1
不等式成立,
2* 设n=k时(k≥3),有2k>2k+1
则 2k+1>2(2k+1)
=4k+2
=2(k+1)+1+(2k-1).
∵k≥3,∴2k-1>0.
从而 2k+1>2(k+1)+1+(2k-1)
>2(k+1)+1
即 n=k+1时,亦有 2n>2n+1.
综上1*、2*知,2n>2n+1 对n≥3,n∈N* 都成立。
∴n≥3时,有![]()
综上 n=1时,![]()
n=2时,![]()
n≥3时,![]()


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源:2015届浙江省宁波市高一下学期期中考试文科数学试卷(解析版) 题型:解答题
已知数列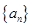 的首项
的首项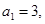 前
前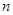 项和为
项和为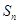 ,且
,且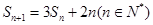 ,
,
(1)试判断数列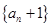 是否成等比数列?并求出数列
是否成等比数列?并求出数列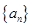 的通项公式;
的通项公式;
(2)记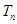 为数列
为数列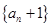 前
前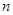 项和,求
项和,求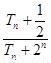 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com