
【题目】已知8件不同的产品中有3件次品,现对它们一一进行测试,直至找到所有次品.
(1)若在第5次测试时找到最后一件次品,则共有多少种不同的测试方法?
(2)若至多测试5次就能找到所有次品,则共有多少种不同的测试方法?
【答案】(1)720种(2)936种
【解析】
(1)由题意可知前四次中有两件次品两件正品,第五次为次品,所以选出排列即可. (2)至多五次能找到,包括检测3次都是次品,检测四次测出3件次品,检测五次测出3件次品或着检测五次全是正品,剩下的为次品,以此求出每种情况求和可得结果.
解:(1)若在第五次检测出最后一件次品,则前四次中有两件次品两件正品,第五次为次品.
则不同的检测方法共有![]() 种.
种.
(2)检测3次可测出3件次品,不同的测试方法有![]() 种
种
检测4次可测出3件次品,不同的测试方法有![]() 种;
种;
检测5次测出3件次品,分为两类:一类是恰好第5次测到次品,一类是前5次测到都是正品,不同的测试方法共有![]() 种.所以共有936种测试方法
种.所以共有936种测试方法


科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁、戊和己6人围坐在一张正六边形的小桌前,每边各坐一人.已知:①甲与乙正面相对;②丙与丁不相邻,也不正面相对.若己与乙不相邻,则以下选项正确的是( )
A.若甲与戊相邻,则丁与己正面相对B.甲与丁相邻
C.戊与己相邻D.若丙与戊不相邻,则丙与己相邻
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对定义在[0,1]上,并且同时满足以下两个条件的函数f(x)称为G函数.
①对任意的x∈[0,1],总有f(x)≥0;
②当x1≥0,x2≥0,x1+x2≤1时,总有f(x1+x2)≥f(x1)+f(x2)成立.已知函数g(x)=x2与h(x)=2x﹣b是定义在[0,1]上的函数.
(1)试问函数g(x)是否为G函数?并说明理由;
(2)若函数h(x)是G函数,求实数b组成的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为推动文明城市创建,提升城市整体形象,2018年12月30日盐城市人民政府出台了《盐城市停车管理办法》,2019年3月1日起施行.这项工作有利于市民养成良好的停车习惯,帮助他们树立绿色出行的意识,受到了广大市民的一致好评.现从某单位随机抽取80名职工,统计了他们一周内路边停车的时间t(单位:小时),整理得到数据分组及频率分布直方图如下:


(1)从该单位随机选取一名职工,试估计这名职工一周内路边停车的时间少于8小时的概率;
(2)求频率分布直方图中a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为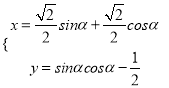 (
(![]() 为参数),若以直角坐标系中的原点为极点,
为参数),若以直角坐标系中的原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() 为实数.)
为实数.)
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 与曲线
与曲线![]() 有公共点,求
有公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四种说法中,
①命题“存在x∈R,x2﹣x>0”的否定是“对于任意x∈R,x2﹣x<0”;
②命题“p且q为真”是“p或q为真”的必要不充分条件;
③已知幂函数f(x)=xα的图象经过点(2,![]() ),则f(4)的值等于
),则f(4)的值等于![]() ;
;
④已知向量a=(3,4),b=(2,1),b =(2,1),则向量a在向量b方向上的投影是![]() ,
,
其中说法正确的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业有2个分厂生产某种零件,为了研究两个分厂生产零件的质量是否有差异,随机从2个分厂生产的零件中各抽取了500件,具体数据如下表所示:
甲厂 | 乙厂 | 总计 | |
优质品 | 360 | 320 | 680 |
非优质品 | 140 | 180 | 320 |
总计 | 500 | 500 | 1000 |
根据表中数据得![]() 的观测值
的观测值![]() ,从而断定两个分厂生产零件的质量有差异,那么这种判断出错的最大可能性为( )
,从而断定两个分厂生产零件的质量有差异,那么这种判断出错的最大可能性为( )
附表:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
A.0.1B.0.01C.0.05D.0.001
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com