
【题目】已知函数![]() 是
是![]() 上的偶函数.
上的偶函数.
(1)求![]() 值;
值;
(2)解![]() 的不等式的解集;
的不等式的解集;
(3)若关于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)a=1;(2)(﹣2,2);(3)![]() .
.
【解析】
(1)根据函数的奇偶性求出a的值即可;
(2)设2x=t,则不等式即为![]() ,再解关于x的不等式即可;
,再解关于x的不等式即可;
(3)问题转化为m![]() 在(0,+∞)恒成立,设t=2x,(t>1),则m
在(0,+∞)恒成立,设t=2x,(t>1),则m![]() 在t>1恒成立,从而求出m的范围即可.
在t>1恒成立,从而求出m的范围即可.
(1)∵f(x)为偶函数,
∴f(﹣x)=f(x)恒成立,
∴f(﹣x)﹣f(x)=0恒成立,
∴![]() ,恒成立,
,恒成立,
即![]() 恒成立,
恒成立,
![]() ,
,
∵a>0,∴a=1,∴a=1;
(2)由(1)知![]() ,
,
设2x=t,则不等式即为![]() ,
,
∴![]() ,
,
所以原不等式解集为(﹣2,2);
(3)f(x)=2x+2﹣x﹣1,
mf(x)≥2﹣x﹣m,
即m![]() 在(0,+∞)恒成立,
在(0,+∞)恒成立,
设t=2x,(t>1),则m![]() 在t>1恒成立,
在t>1恒成立,
又y![]() 在t>1单调递减,得
在t>1单调递减,得![]()
故![]() .
.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C所对的边分别为a,b,c.向量![]() =(a,
=(a,![]() b)与
b)与![]() =(cosA,sinB)平行.
=(cosA,sinB)平行.
(1)求A;
(2)若a=![]() ,b=2,求△ABC的面积.
,b=2,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
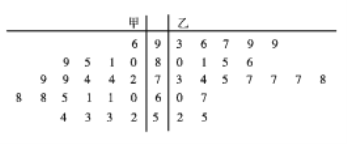
【题目】为推行“新课堂”教学法,某老师分别用传统教学和“新课堂”两种不同的教学方式在甲、乙两个平行班进行教学实验,为了解教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,作出如图所示的茎叶图,若成绩大于70分为“成绩优良”.
(1)由统计数据填写下面2×2列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“成绩优良与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优良 | |||
成绩不优良 | |||
总计 |
(2)从甲、乙两班40个样本中,成绩在60分以下(不含60分)的学生中任意选取2人,求抽取的2人中恰有一人来自乙班的概率.
|
|
|
|
|
|
|
|
|
|
附:![]() ,(
,(![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() ,下列结论中错误的是
,下列结论中错误的是
A. ![]()
![]() , f(
, f(![]() )=0
)=0
B. 函数y=f(x)的图像是中心对称图形
C. 若![]() 是f(x)的极小值点,则f(x)在区间(-∞,
是f(x)的极小值点,则f(x)在区间(-∞,![]() )单调递减
)单调递减
D. 若![]() 是f(x)的极值点,则
是f(x)的极值点,则![]() (
(![]() )=0
)=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在甲地,随着人们生活水平的不断提高,进入电影院看电影逐渐成为老百姓的一种娱乐方式.我们把习惯进入电影院看电影的人简称为“有习惯”的人,否则称为“无习惯的人”.某电影院在甲地随机调查了100位年龄在15岁到75岁的市民,他们的年龄的频数分布和“有习惯”的人数如下表:

(1)以年龄45岁为分界点,请根据100个样本数据完成下面![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为“有习惯”的人与年龄有关;
的把握认为“有习惯”的人与年龄有关;

(2)已知甲地从15岁到75岁的市民大约有11万人,以频率估计概率,若每张电影票定价为![]() 元
元![]() ,则在“有习惯”的人中约有
,则在“有习惯”的人中约有![]() 的人会买票看电影(
的人会买票看电影(![]() 为常数).已知票价定为30元的某电影,票房达到了 69.3万元.某新影片要上映,电影院若将电影票定价为25元,那么该影片票房估计能达到多少万元?
为常数).已知票价定为30元的某电影,票房达到了 69.3万元.某新影片要上映,电影院若将电影票定价为25元,那么该影片票房估计能达到多少万元?
参考公式:![]() ,其中
,其中![]() .
.
参考临界值

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com