
【题目】如图,三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD .

(1)求证:CD⊥平面ABD;
(2)若AB=BD=CD=1,M为AD中点,求三棱锥A-MBC的体积.
【答案】(1)详见解析(2)![]()
【解析】试题分析:(Ⅰ)证明:CD⊥平面ABD,只需证明AB⊥CD;(Ⅱ)利用转换底面,VA-MBC=VC-ABM=![]() S△ABMCD,即可求出三棱锥A-MBC的体积
S△ABMCD,即可求出三棱锥A-MBC的体积
试题解析:(1)∵AB⊥平面BCD,CD平面BCD,
∴AB⊥CD.
又∵CD⊥BD,AB∩BD=B,
AB平面ABD,BD平面ABD,
∴CD⊥平面ABD.
(2)法一:由AB⊥平面BCD,得AB⊥BD,
∵AB=BD=1,∴S△ABD=![]() .
.
∵M是AD的中点,
∴S△ABM=![]() S△ABD=
S△ABD=![]()
由(1)知,CD⊥平面ABD,
∴三棱锥C-ABM的高h=CD=1,
因此三棱锥A-MBC的体积
VA-MBC=VC-ABM=![]() S△ABM·h=
S△ABM·h=![]() .
.
法二:由AB⊥平面BCD知,平面ABD⊥平面BCD,又平面ABD∩平面BCD=BD,如图,过点M作MN⊥BD交BD于点N,则MN⊥平面BCD,且MN=![]() AB=
AB=![]() ,又CD⊥BD,BD=CD=1,
,又CD⊥BD,BD=CD=1,
∴S△BCD=![]() .
.
∴三棱锥A-MBC的体积
VA-MBC=VA-BCD-VM-BCD
=![]() AB·S△BCD-
AB·S△BCD-![]() MN·S△BCD
MN·S△BCD
=![]() .
.



科目:高中数学 来源: 题型:
【题目】(本小题满分14分)
如图,四边形![]() 是正方形,△
是正方形,△![]() 与△
与△![]() 均是以
均是以![]() 为直角顶点的等腰直角三角形,点
为直角顶点的等腰直角三角形,点![]() 是
是![]() 的中点,点
的中点,点![]() 是边
是边![]() 上的任意一点.
上的任意一点.
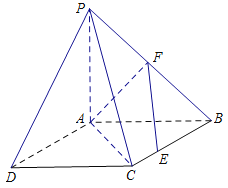
(1)求证: ![]() ;
;
(2)求二面角![]() 的平面角的正弦值.
的平面角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
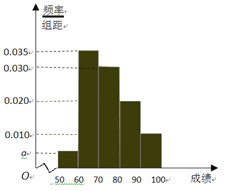
【题目】某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下:
组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均分;
(3)现用分层抽样的方法从第3、4、5组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD-A1B1C1D1中,E,F,P,Q,M,N分别是棱AB,AD,DD1,BB1,A1B1,A1D1的中点.求证:
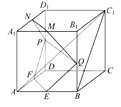
(1)直线BC1∥平面EFPQ.
(2)直线AC1⊥平面PQMN.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,直线![]() 的参数方程为
的参数方程为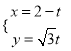 (t为参数),P、Q分别为直线
(t为参数),P、Q分别为直线![]() 与x轴、y轴的交点,线段PQ的中点为M.
与x轴、y轴的交点,线段PQ的中点为M.
(Ⅰ)求直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,求点M的极坐标和直线OM的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】.如图,在三棱锥V-ABC中,VO⊥平面ABC,O∈CD,VA=VB,AD=BD,则下列结论中不一定成立的是 ( )
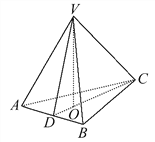
A. AC=BC
B. VC⊥VD
C. AB⊥VC
D. S△VCD·AB=S△ABC·VO
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知e为自然对数的底数,设函数![]() ,则( ).
,则( ).
A. 当k=1时,f(x)在x=1处取到极小值 B. 当k=1时,f(x)在x=1处取到极大值
C. 当k=2时,f(x)在x=1处取到极小值 D. 当k=2时,f(x)在x=1处取到极大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线C1![]() (t为参数),C2
(t为参数),C2 ![]() (θ为参数),
(θ为参数),
(Ⅰ)当α=![]() 时,求C1与C2的交点坐标;
时,求C1与C2的交点坐标;
(Ⅱ)过坐标原点O做C1的垂线,垂足为A,P为OA中点,当α变化时,求P点的轨迹的参数方程,并指出它是什么曲线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com