
【题目】已知抛物线![]() 的焦点在抛物线
的焦点在抛物线![]() 上,点
上,点![]() 是抛物线
是抛物线![]() 上的动点.
上的动点.
(1)求抛物线![]() 的方程及其准线方程;
的方程及其准线方程;
(2)过点![]() 作抛物线
作抛物线![]() 的两条切线,
的两条切线,![]() 、
、![]() 分别为两个切点,求
分别为两个切点,求![]() 面积的最小值.
面积的最小值.
【答案】(1)![]() 的方程为
的方程为![]() 其准线方程为
其准线方程为![]() ;(2)2
;(2)2
【解析】试题分析:(1)求得抛物线C1的焦点,由题意可得p=2,即可得到所求抛物线的方程和准线方程;(2)设P(2t,t2),A(x1,y1),B(x2,y2),求出y=x2+1的导数,可得切线PA,PB的斜率和方程,又PA和PB都过P点,可得直线AB的方程,代入抛物线y=x2+1,运用韦达定理和弦长公式,由点到直线的距离公式,可得P到直线AB的距离,再由三角形的面积公式,化简整理计算可得所求面积的最小值.
试题解析:
(1)![]() 的方程为
的方程为![]() 其准线方程为
其准线方程为![]() .
.
(2)设![]() ,
,![]() ,
,![]() ,
,
则切线![]() 的方程:
的方程:![]() ,即
,即![]() ,又
,又![]() ,
,
所以![]() ,同理切线
,同理切线![]() 的方程为
的方程为![]() ,
,
又![]() 和
和![]() 都过
都过![]() 点,所以
点,所以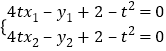 ,
,
所以直线![]() 的方程为
的方程为![]() .
.
联立![]() 得
得![]() ,所以
,所以![]() 。
。
所以![]() .
.
点![]() 到直线
到直线![]() 的距离
的距离![]() .
.
所以![]() 的面积
的面积![]()
所以当![]() 时,
时, ![]() 取最小值为
取最小值为![]() 。即
。即![]() 面积的最小值为2.
面积的最小值为2.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在“新零售”模式的背景下,某大型零售公司为推广线下分店,计划在![]() 市
市![]() 区开设分店,为了确定在该区设分店的个数,该公司对该市开设分店的其他区的数据做了初步处理后得到下列表格.记
区开设分店,为了确定在该区设分店的个数,该公司对该市开设分店的其他区的数据做了初步处理后得到下列表格.记![]() 表示在各区开设分店的个数,
表示在各区开设分店的个数,![]() 表示这
表示这![]() 个分店的年收入之和.
个分店的年收入之和.

(1)该公司已经过初步判断,可用线性回归模型拟合![]() 与
与![]() 的关系,求
的关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)假设该公司在![]() 区获得的总年利润
区获得的总年利润![]() (单位:百万元)与
(单位:百万元)与![]() ,
,![]() 之间的关系为
之间的关系为![]() ,请结合(1)中的线性回归方程,估算该公司在
,请结合(1)中的线性回归方程,估算该公司在![]() 区开设多少个分店时,才能使
区开设多少个分店时,才能使![]() 区平均每个分店的年利润最大?
区平均每个分店的年利润最大?
参考公式:回归直线方程为![]() ,其中
,其中 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]()
![]() 上的任一点到焦点的距离最大值为3,离心率为
上的任一点到焦点的距离最大值为3,离心率为![]() ,
,
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 为曲线
为曲线![]() 上两点,
上两点, ![]() 为坐标原点,直线
为坐标原点,直线![]() 的斜率分别为
的斜率分别为![]() ,且
,且![]() ,求直线
,求直线![]() 被圆
被圆![]() 截得弦长的最大值及此时直线
截得弦长的最大值及此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 的顶点是原点,以
的顶点是原点,以![]() 轴为对称轴,且经过点
轴为对称轴,且经过点![]() .
.
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)设点![]() ,
, ![]() 在抛物线
在抛物线![]() 上,直线
上,直线![]() ,
, ![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,
, ![]() ,
, ![]() .求直线
.求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018四川南充高三第二次(3月)高考适应性考试】某校开展“翻转合作学习法”教学试验,经过一年的实践后,对“翻转班”和“对照班”的全部220名学生的数学学习情况进行测试,按照大于或等于120分为“成绩优秀”,120分以下为“成绩一般”统计,得到如下的![]() 列联表:
列联表:
成绩优秀 | 成绩一般 | 合计 | |
对照班 | 20 | 90 | 110 |
翻转班 | 40 | 70 | 110 |
合计 | 60 | 160 | 220 |
(I)根据上面的列联表判断,能否在犯错误的概率不超过0.001的前提下认为“成绩优秀与翻转合作学习法”有关;
(II)为了交流学习方法,从这次测试数学成绩优秀的学生中,用分层抽样方法抽出6名学生,再从这6名学生中抽3名出来交流学习方法,求至少抽到1名“对照班”学生交流的概率.
附表:![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校倡导为特困学生募捐,要求在自动购水机处每购买一瓶矿泉水,便自觉向捐款箱中至少投入一元钱.现统计了连续5天的售出矿泉水箱数和收入情况,列表如下:
售出水量 | 7 | 6 | 6 | 5 | 6 |
收入 | 165 | 142 | 148 | 125 | 150 |
学校计划将捐款以奖学金的形式奖励给品学兼优的特困生,规定:特困生综合考核前20名,获一等奖学金500元;综合考核21-50名,获二等奖学金300元;综合考核50名以后的不获得奖学金.
(1)若![]() 与
与![]() 成线性相关,则某天售出9箱水时,预计收入为多少元?
成线性相关,则某天售出9箱水时,预计收入为多少元?
(2)甲乙两名学生获一等奖学金的概率均为![]() ,获二等奖学金的概率均为
,获二等奖学金的概率均为![]() ,不获得奖学金的概率均为
,不获得奖学金的概率均为![]() ,已知甲乙两名学生获得哪个等级的奖学金相互独立,求甲乙两名学生所获得奖学金之和
,已知甲乙两名学生获得哪个等级的奖学金相互独立,求甲乙两名学生所获得奖学金之和![]() 的分布列及数学期望;
的分布列及数学期望;
附:回归方程![]() ,其中
,其中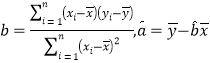 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
, ![]() 满足约束条件
满足约束条件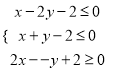 ,若
,若![]() 取得最大值的最优解不唯一,则实数
取得最大值的最优解不唯一,则实数![]() 的值为__________.
的值为__________.
【答案】![]() 或
或![]()
【解析】由题可知若![]() 取得最大值的最优解不唯一则
取得最大值的最优解不唯一则![]() 必平行于可行域的某一边界,如图:
必平行于可行域的某一边界,如图: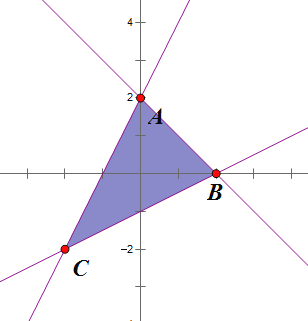 要Z最大则直线与y轴的截距最大即可,当a<0时,则平行AC直线即可故a=-2,当a>0时,则直线平行AB即可,故a=1
要Z最大则直线与y轴的截距最大即可,当a<0时,则平行AC直线即可故a=-2,当a>0时,则直线平行AB即可,故a=1
点睛:线性规划为常考题型,解决此题务必要理解最优解个数为无数个时的条件是什么,然后根据几何关系求解即可
【题型】填空题
【结束】
16
【题目】《数书九章》三斜求积术:“以小斜幂,并大斜幂,减中斜幂,余半之,自乘于上;以小斜幂乘大斜幂,减上,余四约一,为实,一为从隅,开平方得积”.秦九韶把三角形的三条边分别称为小斜、中斜和大斜,“术”即方法.以![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别表示三角形的面积,大斜,中斜,小斜;
分别表示三角形的面积,大斜,中斜,小斜; ![]() ,
, ![]() ,
, ![]() 分别为对应的大斜,中斜,小斜上的高;则
分别为对应的大斜,中斜,小斜上的高;则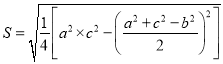
![]()
![]() .若在
.若在![]() 中
中![]() ,
, ![]() ,
, ![]() ,根据上述公式,可以推出该三角形外接圆的半径为__________.
,根据上述公式,可以推出该三角形外接圆的半径为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com