
【题目】已知抛物线![]() :
:![]() 的焦点
的焦点![]() 是椭圆
是椭圆![]() 的一个焦点.
的一个焦点.
(1)求抛物线![]() 的方程;
的方程;
(2)设![]() ,
,![]() ,
,![]() 为抛物线
为抛物线![]() 上的不同三点,点
上的不同三点,点![]() ,且
,且![]() .求证:直线
.求证:直线![]() 过定点.
过定点.
科目:高中数学 来源: 题型:
【题目】勒洛三角形是具有类似圆的“定宽性”的曲线,它是由德国机械工程专家、机构运动学家勒洛首先发现,其作法是:以等边三角形每个顶点为圆心,以边长为半径,在另两个顶点间作一段弧,三段弧围成的曲边三角形就是勒洛三角形.如图中的两个勒洛三角形,它们所对应的等边三角形的边长比为![]() ,若从大的勒洛三角形中随机取一点,则此点取自小勒洛三角形内的概率是( )
,若从大的勒洛三角形中随机取一点,则此点取自小勒洛三角形内的概率是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.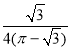
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的是( )
A.若两个随机变量的线性相关性越强,则相关系数![]() 的值越接近于1
的值越接近于1
B.设有一个回归方程![]() ,变量
,变量![]() 增加一个单位时,
增加一个单位时,![]() 平均增加5个单位
平均增加5个单位
C.把某中学的高三年级560名学生编号:1到560,再从编号为1到10的10名学生中随机抽取1名学生,其编号为![]() ,然后抽取编号为
,然后抽取编号为![]() ,
,![]() ,
,![]() ,…的学生,这样的抽样方法是分层抽样
,…的学生,这样的抽样方法是分层抽样
D.若一组数据0,![]() ,3,4的平均数是2,则该组数据的方差是
,3,4的平均数是2,则该组数据的方差是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
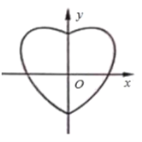
【题目】数学中有许多形状优美,寓意美好的曲线,曲线C:![]() 就是其中之一(如图).给出下列三个结论:
就是其中之一(如图).给出下列三个结论:
①曲线C恰好经过6个整点(即横、纵坐标均为整数的点);
②曲线C上存在到原点的距离超过![]() 的点;
的点;
③曲线C所围成的“心形”区域的面积小于3.其中所有正确结论的个数是( ).
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,四点
,四点![]() ,
,![]() ,
,![]() ,
,![]() 中恰有三个点在椭圆
中恰有三个点在椭圆![]() 上,左、右焦点分别为
上,左、右焦点分别为![]() 、
、![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过左焦点![]() 且不与坐标轴平行的直线
且不与坐标轴平行的直线![]() 交椭圆于
交椭圆于![]() 、
、![]() 两点,若线段
两点,若线段![]() 的垂直平分线交
的垂直平分线交![]() 轴于点
轴于点![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图:在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 上一点,
上一点,![]() 是
是![]() 的延长线与
的延长线与![]() 的延长线的交点,且
的延长线的交点,且![]() 平面
平面![]() .
.
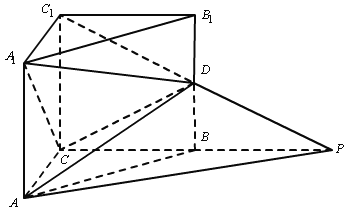
(1)求证:![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)若点![]() 在线段
在线段![]() 上,且直线
上,且直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一个正四面体和一个正四棱锥,它们的各条棱长均相等,则下列说法:
①它们的高相等;②它们的内切球半径相等;③它们的侧棱与底面所成的线面角的大小相等;④若正四面体的体积为![]() ,正四棱锥的体积为
,正四棱锥的体积为![]() ,则
,则![]() ;⑤它们能拼成一个斜三棱柱.其中正确的个数为( )
;⑤它们能拼成一个斜三棱柱.其中正确的个数为( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com