练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，两个正方形ABCD和ADEF所在平面互相垂直，设M、N分别是BD和AE的中点，那么①AD⊥MN；②MN∥平面CDE；③MN∥CE；④MN、CE异面．其中假命题的个数为（ ）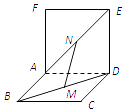

    A.4
    B.3
    C.2
    D.1

    【答案】D
    【解析】解：∵两个正方形ABCD和ADEF所在平面互相垂直，M、N分别是BD和AE的中点，

    取AD的中点G，连接MG，NG，易得AD⊥平面MNG，进而得到AD⊥MN，故①正确；

    连接AC，CE，根据三角形中位线定理，可得MN∥CE，由线面平行的判定定理，可得②MN∥面CDE及③MN∥CE正确，④MN、CE错误；

    ∴其中假命题的个数为：1

    所以答案是：D

    【考点精析】本题主要考查了命题的真假判断与应用的相关知识点，需要掌握两个命题互为逆否命题，它们有相同的真假性；两个命题为互逆命题或互否命题，它们的真假性没有关系才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知m∈R，n∈R，并且m+3n=1，则mem+3ne3n的最小值 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设曲线y=xn+1（n∈N*）在点（1，1）处的切线与x轴的交点的横坐标为xn ， 令an=lgxn ， 则a1+a2+…+a99的值为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】有4个不同的球，4个不同的盒子，把球全部放入盒子内．
    （1）共有几种放法？
    （2）恰有1个空盒，有几种放法？
    （3）恰有2个盒子不放球，有几种放法？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若函数f（x），g（x）满足 f（x）g（x）dx=0，则f（x），g（x）为区间[﹣1，1]上的一组正交函数，给出三组函数： ①f（x）=sin x，g（x）=cos x；
    ②f（x）=x+1，g（x）=x﹣1；
    ③f（x）=x，g（x）=x2 ，
    其中为区间[﹣1，1]上的正交函数的组数是（ ）
    A.0
    B.1
    C.2
    D.3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若不等式ax2﹣bx+c＞0的解集为{x|﹣2＜x＜3}，求不等式cx2﹣bx﹣a＜0的解集．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了培养学生的数学建模和应用能力，某校组织了一次实地测量活动，如图，假设待测量的树木AE的高度H（m），垂直放置的标杆BC的高度h=4m，仰角∠ABE=α，∠ADE=β（D，C，E三点共线），试根据上述测量方案，回答如下问题：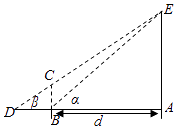

    （1）若测得α=60°、β=30°，试求H的值；
    （2）经过分析若干次测得的数据后，大家一致认为适当调整标杆到树木的距离d（单位：m），使α与β之差较大时，可以提高测量精确度．
    若树木的实际高度为8m，试问d为多少时，α﹣β最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如果曲线2|x|﹣y﹣4=0与曲线x2+λy2=4（λ＜0）恰好有两个不同的公共点，则实数λ的取值范围是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示是一个三棱台ABC－A′B′C′，试用两个平面把这个三棱台分成三部分，使每一部分都是一个三棱锥．

    查看答案和解析>>

    同步练习册答案