
 中,四边形
中,四边形 是正方形,
是正方形, 为CE上的点,且
为CE上的点,且 平面
平面 .
. 平面
平面 ;
; 的余弦值.
的余弦值.
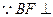 平面
平面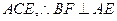 ………………2分
………………2分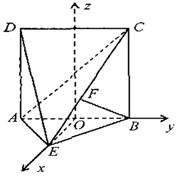
 为直二面角,且
为直二面角,且 ,
, 平面
平面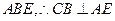 ………………4分
………………4分
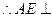 平面
平面 .………………6分
.………………6分 与
与 交于
交于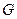 ,连接FG,设正方形ABCD的边长为2,
,连接FG,设正方形ABCD的边长为2,  ,………………7分
,………………7分 垂直于平面
垂直于平面 ,由三垂线定理逆定理得
,由三垂线定理逆定理得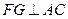
 是二面角
是二面角 的平面角………………9分
的平面角………………9分 平面
平面 ,
, .
. 中,
中, ………………10分
………………10分
 ,则
,则
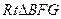 中,
中,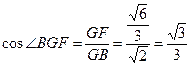
 的余弦值为
的余弦值为 .………………14分
.………………14分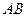 之中点
之中点 为坐标原点建立空间坐标系
为坐标原点建立空间坐标系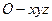 ,………………7分
,………………7分
 ……………8分
……………8分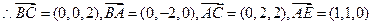 ,………9分
,………9分 的法向量分别为
的法向量分别为 ,则由
,则由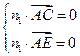 得
得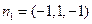 ,
,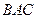 的一个法向量
的一个法向量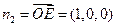 ………………11分
………………11分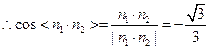 ………………13分
………………13分 为锐角,
为锐角, 的余弦值为
的余弦值为 .…………14分
.…………14分

 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:高中数学 来源:不详 题型:解答题
 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 中,平面
中,平面 侧面
侧面 .
. ;
; 与平面
与平面 所成角是
所成角是 ,锐二面角
,锐二面角 的平面角是
的平面角是 ,试判断
,试判断 与
与 的大小关系,并予以证明.
的大小关系,并予以证明.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 BCD与直角梯形ADEF所
BCD与直角梯形ADEF所 垂直,∠ADE=90°,AF∥DE,DE=DA=2AF=2。
垂直,∠ADE=90°,AF∥DE,DE=DA=2AF=2。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com