
分析 由条件利用正弦定理可得20a•$\overrightarrow{BC}$+15b•$\overrightarrow{CA}$+12c•$\overrightarrow{AB}$=$\overrightarrow{0}$,化简可得可得15b-20a=0,且12c-20a=0,求得c2-b2=a2,故△ABC为直角三角形.
解答 解:△ABC中,由20sinA•$\overrightarrow{BC}$+15sinB•$\overrightarrow{CA}$+12sinC•$\overrightarrow{AB}$=$\overrightarrow{0}$,
利用正弦定理得20a•$\overrightarrow{BC}$+15b•$\overrightarrow{CA}$+12c•$\overrightarrow{AB}$=$\overrightarrow{0}$,
又$\overrightarrow{BC}=\overrightarrow{BA}+\overrightarrow{AC}=-(\overrightarrow{AB}+\overrightarrow{CA})$,
故(15b-20a)$\overrightarrow{CA}$+(12c-20a)$\overrightarrow{AB}$=$\overrightarrow{0}$.
由$\overrightarrow{CA}$,$\overrightarrow{AB}$为不共线向量,可得15b-20a=0,且12c-20a=0,
所以b=$\frac{4}{3}$a,c=$\frac{5}{3}$a,从而c2-b2=a2,故△ABC为直角三角形.
故答案为:直角三角形.
点评 本题主要考查两个向量的数量积的运算,正弦定理的应用,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
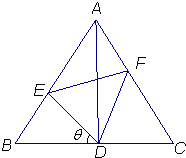 如图,已知△ABC是边长为4的正三角形,D是BC的中点,E,F分别是边AB,AC上的点,且∠EDF=$\frac{π}{3}$,设∠BDE=θ$(\frac{π}{6}<θ<\frac{π}{2})$.
如图,已知△ABC是边长为4的正三角形,D是BC的中点,E,F分别是边AB,AC上的点,且∠EDF=$\frac{π}{3}$,设∠BDE=θ$(\frac{π}{6}<θ<\frac{π}{2})$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{36}$ | B. | $\frac{1}{12}$ | C. | $\frac{5}{21}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 合格品 | 次品 | 总计 | |
| 甲机床加工的零件数 | 35 | 5 | 40 |
| 乙机床加工的零件数 | 50 | 10 | 60 |
| 总计 | 85 | 15 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com