Question

【题目】某种水箱用的“浮球”是由两个相同半球和一个圆柱筒组成，它的轴截面如图所示，已知半球的直径是，圆柱筒高，为增强该“浮球”的牢固性，给“浮球”内置一“双蝶形”防压卡，防压卡由金属材料杆,,,,,及焊接而成，其中,分别是圆柱上下底面的圆心，，，，均在“浮球”的内壁上，AC，BD通过“浮球”中心，且、均与圆柱的底面垂直．

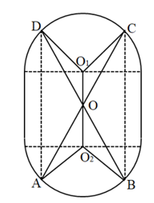
（1）设与圆柱底面所成的角为，试用表示出防压卡中四边形的面积，并写出的取值范围；

（2）研究表明，四边形的面积越大，“浮球”防压性越强，求四边形面积取最大值时，点到圆柱上底面的距离．

Answer 1

【答案】（1），其中的取值范围是（2）四边形面积取最大值时，点到圆柱上底面的距离为.

【解析】

（1）先证明，又因为，则四边形是梯形，用与圆柱底面所成的角来表示梯形的上底、下底和高，根据梯形面积公式即可求得四边形面积；

（２）由（1）得四边形面积的解析式，对函数求导，判断单调性，求出极值点，由此得出点到圆柱上底面的距离.

解:（1）因为分别是圆柱上、下底面的圆心,所以与圆柱的底面垂直；

因为与圆柱的底面垂直,所以；

在梯形中, , ,

设梯形的高；

所以梯形的面积为

其中的取值范围是；

（2）由（1）得,

,

令,解得 或（不合题意,舍去）；

又,所以 ；

列表如下；

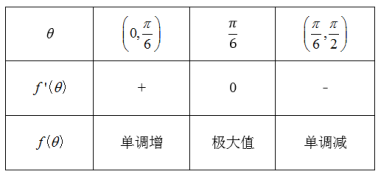
所以当时, 取得极大值,即是最大值,此时；

所以四边形面积取最大值时,点到圆柱上底面的距离为．