
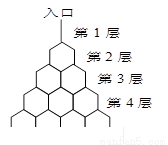
 如图是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有第一条的为第一层,有二条的为第二层,…,依此类推.现有一颗小弹子从第一层的通道里向下运动.记小弹子落入第n层第m个竖直通道(从左至右)的概率为P(n,m).(已知在通道的分叉处,小弹子以相同的概率落入每个通道)
如图是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有第一条的为第一层,有二条的为第二层,…,依此类推.现有一颗小弹子从第一层的通道里向下运动.记小弹子落入第n层第m个竖直通道(从左至右)的概率为P(n,m).(已知在通道的分叉处,小弹子以相同的概率落入每个通道)
|
| C | 0 1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| C | 1 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2n-1 |
2
| ||
| 25 |
| 2 |
| 32 |
| ||
| 25 |
| 10 |
| 32 |
2
| ||
| 25 |
| 20 |
| 32 |
| ξ | 3 | 2 | 1 | ||||||
| P |
|
|
|
| 2 |
| 32 |
| 10 |
| 32 |
| 20 |
| 32 |
| 23 |
| 16 |


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
 如图是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有第一条的为第一层,有二条的为第二层,…,依此类推.现有一颗小弹子从第一层的通道里向下运动.记小弹子落入第n层第m个竖直通道(从左至右)的概率为P(n,m).(已知在通道的分叉处,小弹子以相同的概率落入每个通道)
如图是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有第一条的为第一层,有二条的为第二层,…,依此类推.现有一颗小弹子从第一层的通道里向下运动.记小弹子落入第n层第m个竖直通道(从左至右)的概率为P(n,m).(已知在通道的分叉处,小弹子以相同的概率落入每个通道)
|
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省八市高三三月调考理科数学试卷(解析版) 题型:解答题
如图是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有一条的为第一层,有二条的为第二层, ,依次类推.现有一颗小弹子从第一层的通道里向下运动,若在通道的分叉处,小弹子以相同的概率落入每个通道.记小弹子落入第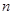 层第
层第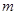 个竖直通道(从左至右)的概率为
个竖直通道(从左至右)的概率为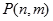 ,某研究性学习小组经探究发现小弹子落入第
,某研究性学习小组经探究发现小弹子落入第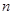 层的第
层的第 个通道的次数服从二项分布,请你解决下列问题.
个通道的次数服从二项分布,请你解决下列问题.
(Ⅰ)试求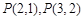 及
及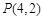 的值,并猜想
的值,并猜想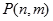 的表达式;(不必证明)
的表达式;(不必证明)
(Ⅱ)设小弹子落入第6层第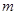 个竖直通道得到分数为
个竖直通道得到分数为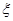 ,其中
,其中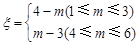 ,试求
,试求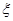 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省八市高三3月联考理科数学试卷(解析版) 题型:解答题
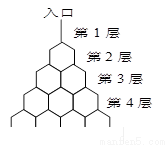
(本题满分12分)如图是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有一条的为第一层,有二条的为第二层,…,依次类推.现有一颗小弹子从第一层的通道里向下运动,若在通道的分叉处,小弹子以相同的概率落入每个通道.记小弹子落入第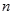 层第
层第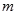 个竖直通道(从左至右)的概率为
个竖直通道(从左至右)的概率为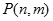 ,某研究性学习小组经探究发现小弹子落入第
,某研究性学习小组经探究发现小弹子落入第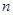 层的第
层的第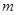 个通道的次数服从二项分布,请你解决下列问题.
个通道的次数服从二项分布,请你解决下列问题.
(Ⅰ)试求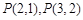 及
及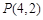 的值,并猜想
的值,并猜想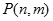 的表达式;(不必证明)
的表达式;(不必证明)
(Ⅱ)设小弹子落入第6层第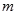 个竖直通道得到分数为
个竖直通道得到分数为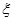 ,其中
,其中 ,试求
,试求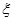 的分布列
的分布列
及数学期望.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省高三2月月考数学理卷 题型:解答题
(本小题满分14分)
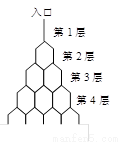
如图是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有第一条的为第一层,有二条的为第二层,……,依次类推.现有一颗小弹子从第一层的通道里向下运动.记小弹子落入第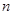 层第
层第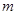 个竖直通道(从左至右)的概率为
个竖直通道(从左至右)的概率为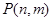 .(已知在通道的分叉处,小弹子以相同的概率落入每个通道)
.(已知在通道的分叉处,小弹子以相同的概率落入每个通道)
(Ⅰ)求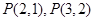 的值,并猜想
的值,并猜想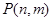 的表达式.(不必证明)
的表达式.(不必证明)
(Ⅱ)设小弹子落入第6层第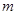 个竖直通道得到分数为
个竖直通道得到分数为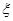 ,其中
,其中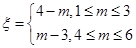 ,试求
,试求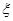 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com