
分析 (Ⅰ)先构造函数g(x)=(1-x)f(x),根据导数和函数最值的关系即可证明;
(Ⅱ)不防设a<b,记g(x)=[f(x)+f(a)](x-a)-2[f(x)-f(a)],分别两次求导,求出函数的最值,即可证明.
解答 证明:(Ⅰ)设g(x)=(1-x)f(x)=(1-x)ex,
∴g′(x)=-xex,
当g′(x)>0时,即x<0,函数g(x)单调递增,
当g′(x)<0时,即x>0,函数g(x)单调递减,
∴g(x)max≥g(0)=1,
∴当x≠0时,(1-x)f(x)<1;
(Ⅱ)不防设a<b
记g(x)=[f(x)+f(a)](x-a)-2[f(x)-f(a)],x≥a
∴g'(x)=f'(x)(x-a)+[f(x)+f(a)]-2f'(x),
=f'(x)(x-a)-[f(x)-f(a)],
∴g″(x)=f″(x)(x-a)+f'(x)-f'(x)=f(x)(x-a)>0,
∴g'(x)在x>a上单调增加,
则g'(x)>g'(a)=0,
∴g(x)在x>a上单调增加,
又g(x)可在x=a处连续,
∴g(x)>g(a)=0,
即[f(x)+f(a)](x-a)-2[f(x)-f(a)]>0,
特别的取x=b,[f(b)+f(a)](b-a)-2[f(b)-f(a)]>0,
整理得$\frac{f(a)-f(b)}{a-b}$<$\frac{f(a)+f(b)}{2}$,
问题得以证明.
点评 本题考查了导数和函数的最值得关系,以及转化思想,构造函数是关键,属于中档题.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源: 题型:选择题
| A. | (-1,1,-1) | B. | (-i,j,-k) | C. | (1,-1,-1) | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1] | B. | (-∞,0] | C. | [0,+∞) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<c<b | B. | a<b<c | C. | c<a<b | D. | b<c<a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 75 | B. | 65 | C. | 60 | D. | 40 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
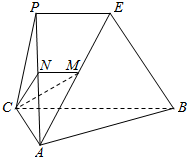 如图,平面PAC⊥平面ABC,AC⊥BC,PE∥CB,M是AE的中点.
如图,平面PAC⊥平面ABC,AC⊥BC,PE∥CB,M是AE的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com