
分析 (1)由已知得(a+b)(1-ab)=0,从而ab=1,由此能求出a=2,b=$\frac{1}{2}$.
(2)由F(x)=f($\sqrt{{x}^{2}-2}$)-g($\sqrt{{x}^{2}-2}$)=log2$\sqrt{{x}^{2}-2}$+$lo{g}_{2}\sqrt{{x}^{2}-2}$=$lo{g}_{2}({x}^{2}-2)$,能求出结果.
解答 解:(1)∵f(x)=1ogax,g(x)=1ogbx,其中正数a,b互不相等且满足a(1-b2)+b(1-a2)=0,
∴a-ab2+b-a2b=(a+b)-ab(a+b)=(a+b)(1-ab)=0,
∴ab=1,
∵f(2)-g(2)=2,
∴$lo{g}_{a}2-lo{g}_{\frac{1}{a}}2$=loga2+loga2=2,
∴loga2=1,解得a=2,∴b=$\frac{1}{2}$.
(2)∵F(x)=f($\sqrt{{x}^{2}-2}$)-g($\sqrt{{x}^{2}-2}$)=log2$\sqrt{{x}^{2}-2}$+$lo{g}_{2}\sqrt{{x}^{2}-2}$=$lo{g}_{2}({x}^{2}-2)$,
∴函数y=F(x)在区间(-∞,-$\sqrt{2}$)上单调递减,在区间($\sqrt{2}$,+∞)上单调递增,
∵函数y=F(x)在区间[m,n]上的值域为[1,1og214],
∴$\left\{\begin{array}{l}{F(m)=lo{g}_{2}({m}^{2}-2)=1}\\{F(n)=lo{g}_{2}({n}^{2}-2)=lo{g}_{2}14}\end{array}\right.$,解得m=2,n=4.
或$\left\{\begin{array}{l}{F(m)=lo{g}_{2}({m}^{2}-2)=lo{g}_{2}14}\\{F(n)=lo{g}_{2}({n}^{2}-2)=1}\end{array}\right.$,解得m=-4,n=-2.
点评 本题考查实数值的求法,是中档题,解题时要认真审题,注意对数函数的性质的合理运用.


科目:高中数学 来源: 题型:解答题
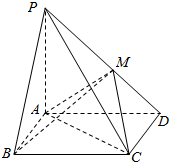 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,AB=1,BM⊥PD于点M.求直线BM与平面ACM所成的角的正弦值.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,AB=1,BM⊥PD于点M.求直线BM与平面ACM所成的角的正弦值.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{3}}{4}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | 3 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,等腰△ABC的一条腰及底边中线分别与圆O相交于点A,D和E、F,圆O的切线FG与CE相交于点G.
如图,等腰△ABC的一条腰及底边中线分别与圆O相交于点A,D和E、F,圆O的切线FG与CE相交于点G.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{ab}}{2}$<$\frac{1}{a}$+$\frac{1}{b}$ | B. | ab≤$\frac{{a}^{2}+{b}^{2}}{2}$ | C. | ab≤($\frac{a+b}{2}$)2 | D. | ($\frac{a+b}{2}$)2≤$\frac{{a}^{2}+{b}^{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
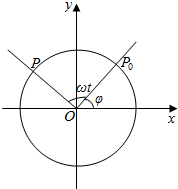 如图,点P是半径为rcm的砂轮边缘上的一个质点,它从初始位置P0开始,按逆时针以角速度ωrαd/s做圆周运动,求点P的纵坐标y关于时间t的函数关系,并求点P的运动周期和频率.
如图,点P是半径为rcm的砂轮边缘上的一个质点,它从初始位置P0开始,按逆时针以角速度ωrαd/s做圆周运动,求点P的纵坐标y关于时间t的函数关系,并求点P的运动周期和频率.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com