
【题目】(本小题满分14分)如图,在四面体![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上,且
上,且![]() .
.
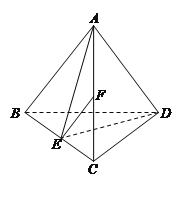
(1)若![]() ∥平面
∥平面![]() ,求实数
,求实数![]() 的值;
的值;
(2)求证:平面![]() 平面
平面![]() .
.
科目:高中数学 来源: 题型:
【题目】哈师大附中高三学年统计甲、乙两个班级一模数学分数(满分150分),每个班级20名同学,现有甲、乙两位同学的20次成绩如下列茎叶图所示:

(I)根据基叶图求甲、乙两位同学成绩的中位数,并将乙同学的成绩的频率分布直方图填充完整;

(Ⅱ)根据基叶图比较甲乙两位同学数学成绩的平均值及稳定程度(不要求计算出具体值,给出结论即可)
(Ⅲ)现从甲乙两位同学的不低于140分的成绩中任意选出2个成绩,设事件![]() 为“其中2 个成绩分别属于不同的同学”,求事件
为“其中2 个成绩分别属于不同的同学”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (a>b>0)的左右焦点分别为F1,F2,图象经过点A(2,0)和点B(0,
(a>b>0)的左右焦点分别为F1,F2,图象经过点A(2,0)和点B(0,![]() )过F2与坐标轴不垂直的直线l与椭圆C交于P,Q两点,N为PQ的中点.
)过F2与坐标轴不垂直的直线l与椭圆C交于P,Q两点,N为PQ的中点.
(1)求椭圆C的方程;
(2)设点![]() ,且MN⊥PQ于N,求直线PQ的方程.
,且MN⊥PQ于N,求直线PQ的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() 的左右焦点
的左右焦点![]() 、
、![]() 恰好是等轴双曲线
恰好是等轴双曲线![]() 的左右顶点,且椭圆的离心率为
的左右顶点,且椭圆的离心率为![]() ,
,![]() 是双曲线
是双曲线![]() 上异于顶点的任意一点,直线
上异于顶点的任意一点,直线![]() 和
和![]() 与椭圆的交点分别记为
与椭圆的交点分别记为![]() 、
、![]() 和
和![]() 、
、![]() .
.
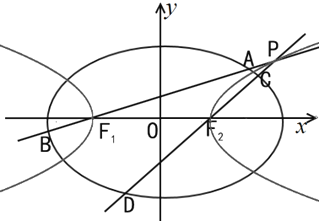
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() ,求证:
,求证:![]() 为定值;
为定值;
(3)若存在点![]() 满足
满足![]() ,试求
,试求![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() ,B为AC的中点,分别以AB,AC为直径在AC的同侧作半圆,M,N分别为两半圆上的动点
,B为AC的中点,分别以AB,AC为直径在AC的同侧作半圆,M,N分别为两半圆上的动点![]() 不含端点A,B,
不含端点A,B,![]() ,且
,且![]() ,则
,则![]() 的最大值为______.
的最大值为______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年,教育部发文确定新高考改革正式启动,湖南、广东、湖北等8省市开始实行新高考制度,从2018年下学期的高一年级学生开始实行.为了适应新高考改革,某校组织了一次新高考质量测评,在成绩统计分析中,高二某班的数学成绩的茎叶图和频率分布直方图因故都受到不同程度的损坏,但可见部分如下,据此解答如下问题:
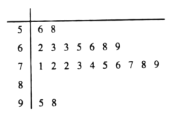
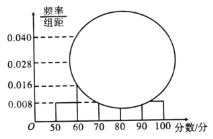
(1)求该班数学成绩在![]() 的频率及全班人数;
的频率及全班人数;
(2)根据频率分布直方图估计该班这次测评的数学平均分;
(3)若规定![]() 分及其以上为优秀,现从该班分数在
分及其以上为优秀,现从该班分数在![]() 分及其以上的试卷中任取
分及其以上的试卷中任取![]() 份分析学生得分情况,求在抽取的
份分析学生得分情况,求在抽取的![]() 份试卷中至少有
份试卷中至少有![]() 份优秀的概率.
份优秀的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD﹣A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内的动点,且A1F∥平面D1AE,记A1F与平面BCC1B1所成的角为θ,下列说法正确的个数是( )
①点F的轨迹是一条线段
②A1F与D1E不可能平行
③A1F与BE是异面直线
④![]()
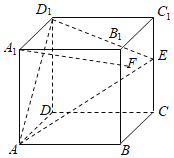
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,射线l:![]() (x≥0),曲线C1的参数方程为
(x≥0),曲线C1的参数方程为![]() (
(![]() 为参数),曲线C2的方程为
为参数),曲线C2的方程为![]() ;以原点为极点,x轴的非负半轴为极轴建立极坐标系,曲线C3的极坐标方程为
;以原点为极点,x轴的非负半轴为极轴建立极坐标系,曲线C3的极坐标方程为![]() .
.
(1)写出射线l的极坐标方程以及曲线C1的普通方程;
(2)已知射线l与C2交于O,M,与C3交于O,N,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在矩形ABCD中,AB=3,BC=4,E,F分别在线段BC,AD上,EF∥AB,将矩形ABEF沿EF折起,记折起后的矩形为MNEF,且平面MNEF⊥平面ECDF.
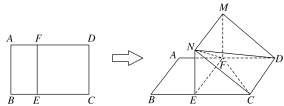
(1)在线段BC是否存在一点E,使得ND⊥FC ,若存在,求出EC的长并证明;
若不存在,请说明理由.
(2)求四面体NEFD体积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com