
| A. | y1=y2 | B. | y1>y2 | C. | y1<y2 | D. | 无法确定 |
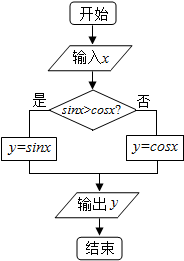
分析 模拟执行程序框图,分别求出输入的x分别为$\frac{5π}{6}$、$\frac{π}{6}$时,相应输出的为y1、y2的值,即可得解.
解答 解:模拟执行程序框图可得:
当输入的x的值为$\frac{5π}{6}$时,sin$\frac{5π}{6}$=$\frac{1}{2}$>cos$\frac{5π}{6}$=-$\frac{\sqrt{3}}{2}$,故输出的y1=sin$\frac{5π}{6}$=$\frac{1}{2}$;
当输入的x的值为$\frac{π}{6}$时,sin$\frac{π}{6}$=$\frac{1}{2}$<cos$\frac{π}{6}$=$\frac{\sqrt{3}}{2}$,故输出的y2=cos$\frac{π}{6}$=$\frac{\sqrt{3}}{2}$;
故可得:y1=$\frac{1}{2}$<y2=$\frac{\sqrt{3}}{2}$.
故选:C.
点评 本题主要考查了三角函数求值及程序框图,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | c<a<b | B. | c<b<a | C. | a<b<c | D. | b<a<c |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
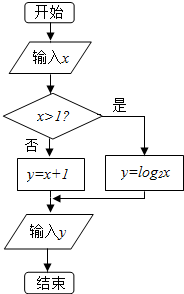
| A. | $\frac{3}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示,一个左右对称的三角形数阵,其第n行共有n个数,每一行的第一个数依次组成等差数列,从第三行起每一行中除了第一个数和最后一个数外,每一个数都等于它肩上的两个数字之和,记第i行的第j个数为f(i,j),则当n≥3时,f(n,2)=$\frac{n(n-1)}{2}+1$.
如图所示,一个左右对称的三角形数阵,其第n行共有n个数,每一行的第一个数依次组成等差数列,从第三行起每一行中除了第一个数和最后一个数外,每一个数都等于它肩上的两个数字之和,记第i行的第j个数为f(i,j),则当n≥3时,f(n,2)=$\frac{n(n-1)}{2}+1$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com