
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() .
.
(1)求椭圆![]() 的方程.
的方程.
(2)设直线![]() 过点
过点![]() 且与椭圆
且与椭圆![]() 交于
交于![]() ,
,![]() 两点.过点
两点.过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() .证明直线
.证明直线![]() 过定点.
过定点.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)由离心率![]() 及
及![]() 可求得
可求得![]() ,得椭圆方程;
,得椭圆方程;
(2)当直线![]() 的斜率存在时,设
的斜率存在时,设![]() ,
,![]() ,
,![]() .直线
.直线![]() :
:![]() ,与椭圆方程联立消元后应用韦达定理得
,与椭圆方程联立消元后应用韦达定理得![]() ,求出直线
,求出直线![]() 方程,再求出
方程,再求出![]() 与
与![]() 交点的横坐标,代入
交点的横坐标,代入![]() 可得其为定值,得定点,直线
可得其为定值,得定点,直线![]() 的斜率不存在时,可直接求出直线
的斜率不存在时,可直接求出直线![]() 方程,也过该定点,从而证得结论成立.
方程,也过该定点,从而证得结论成立.
(1)解:由题意可得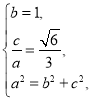 ,解得
,解得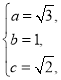 ,
,
所以椭圆![]() 的方程为
的方程为![]() .
.
(2)证明:①当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 的方程为
的方程为![]() ,
,
不妨设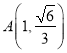 ,
,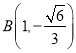 ,
,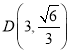 ,
,
此时,直线![]() 的方程为
的方程为![]() ,所以直线
,所以直线![]() 过点
过点![]() .
.
②当直线![]() 的斜率存在时,设
的斜率存在时,设![]() ,
,![]() ,
,![]() .直线
.直线![]() :
:![]() .
.
由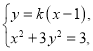 得
得![]() ,
,
所以![]() ,
,![]() .(*)
.(*)
直线![]() :
:![]() ,令
,令![]() ,得
,得![]() ,
,
所以![]() .(**)
.(**)
将(*)代入(**)可得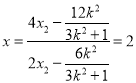 .
.
所以直线![]() 过点
过点![]() .
.
综上所述,直线![]() 过定点
过定点![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱柱![]() 中,底面
中,底面![]() 是正方形,平面
是正方形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() .过顶点
.过顶点![]() ,
,![]() 的平面与棱
的平面与棱![]() ,
,![]() 分别交于
分别交于![]() ,
,![]() 两点.
两点.
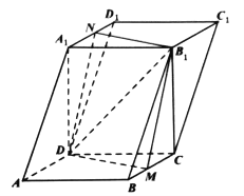
(Ⅰ)求证:![]() ;
;
(Ⅱ)求证:四边形![]() 是平行四边形;
是平行四边形;
(Ⅲ)若![]() ,试判断二面角
,试判断二面角![]() 的大小能否为
的大小能否为![]() ?说明理由.
?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面内两个定点![]() 和点
和点![]() ,
,![]() 是动点,且直线
是动点,且直线![]() ,
,![]() 的斜率乘积为常数
的斜率乘积为常数![]() ,设点
,设点![]() 的轨迹为
的轨迹为![]() .
.
① 存在常数![]() ,使
,使![]() 上所有点到两点
上所有点到两点![]() 距离之和为定值;
距离之和为定值;
② 存在常数![]() ,使
,使![]() 上所有点到两点
上所有点到两点![]() 距离之和为定值;
距离之和为定值;
③ 不存在常数![]() ,使
,使![]() 上所有点到两点
上所有点到两点![]() 距离差的绝对值为定值;
距离差的绝对值为定值;
④ 不存在常数![]() ,使
,使![]() 上所有点到两点
上所有点到两点![]() 距离差的绝对值为定值.
距离差的绝对值为定值.
其中正确的命题是_______________.(填出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加某次知识竞赛的同学中,选取60名同学将其成绩(单位:分.百分制,均为整数)分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题.
六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题.
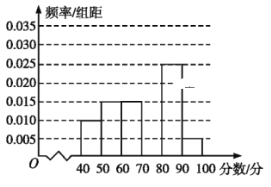
(1)求分数在![]() 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(2)从频率分布直方图中,估计本次考试成绩的众数和平均数;
(3)若从第1组和第6组两组学生中,随机抽取2人,求所抽取2人成绩之差的绝对值大于10的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,有下列四个结论:
,有下列四个结论:
①![]() 为偶函数;②
为偶函数;②![]() 的值域为
的值域为![]() ;
;
③![]() 在
在![]() 上单调递减;④
上单调递减;④![]() 在
在![]() 上恰有8个零点,
上恰有8个零点,
其中所有正确结论的序号为( )
A.①③B.②④C.①②③D.①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四边形![]() 为矩形,
为矩形, ![]() ,
,![]() 为
为![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,得到四棱锥
折起,得到四棱锥![]() ,设
,设![]() 的中点为
的中点为![]() ,在翻折过程中,得到如下有三个命题:
,在翻折过程中,得到如下有三个命题:
①![]() 平面
平面![]() ,且
,且![]() 的长度为定值
的长度为定值![]() ;
;
②三棱锥![]() 的最大体积为
的最大体积为![]() ;
;
③在翻折过程中,存在某个位置,使得![]() .
.
其中正确命题的序号为__________.(写出所有正确结论的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com