
【题目】已知圆C:x2+(y﹣1)2=5,直线l:mx﹣y+1﹣m=0.
(1)判断直线l与圆C的位置关系;
(2)若定点P(1,1)分弦AB为 ![]() =
= ![]() ,求此时直线l的方程.
,求此时直线l的方程.
【答案】
(1)解:由于直线l的方程是mx﹣y+1﹣m=0,即 y﹣1=m(x﹣1),经过定点H(1,1),
而点H到圆心C(0,1)的距离为1,小于半径 ![]() ,故点H在圆的内部,故直线l与圆C相交,
,故点H在圆的内部,故直线l与圆C相交,
故直线和圆恒有两个交点
(2)解:设A(x1,y1),B(x2,y2),由 ![]() =
= ![]() ,得
,得 ![]() =
= ![]()
![]() ,
,
∴1﹣x1= ![]() (x2﹣1),化简的x2=3﹣2x1…①
(x2﹣1),化简的x2=3﹣2x1…①
又由直线代入圆的方程,消去y得:(1+m2)x2﹣2m2x+m2﹣5=0…(*)
∴x1+x2= ![]() …②
…②
由①②解得x1= ![]() 代入(*)式解得m=±1,
代入(*)式解得m=±1,
∴直线l的方程为x﹣y=0或x+y﹣2=0
【解析】(1)根据直线l的方程可得直线经过定点H(1,1),而点H到圆心C(0,1)的距离为1,小于半径,故点H在圆的内部,故直线l与圆C相交,命题得证.(2)把线段的长度比转化为两个向量的关系,由向量的坐标运算得到A,B两点横坐标间的关系,联立直线与圆的方程化为关于x的一元二次方程,由根与系数关系得到A,B两点横坐标的和,求出其中一点的横坐标,最后再代入关于x的方程得到关于m的方程,求解得到m的值,则直线方程可求.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】下面关于集合的表示正确的个数是( )
①{2,3}≠{3,2}; ②{(x , y)|x+y=1}={y|x+y=1};
③{x|x>1}={y|y>1}; ④{x|x+y=1}={y|x+y=1}.
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】利民奶牛场在2016年年初开始改进奶牛饲养方法,同时每月增加一定数目的产奶奶牛,2016年2到5月该奶牛场的产奶量如表所示:
月份 | 2 | 3 | 4 | 5 |
产奶量y(吨) | 2.5 | 3 | 4 | 4.5 |
(1)在给定的坐标系中画出表中数据的散点图; 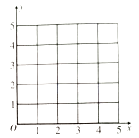
(2)求出y关于x的线性回归方程;
(3)试预测该奶牛场6月份的产奶量? (注:回归方程 ![]() =
= ![]() x+
x+ ![]() 中,
中, ![]() =
= 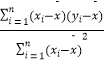 =
= 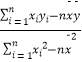 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为一简单组合体,其底面ABCD为正方形,棱PD与EC均垂直于底面ABCD,PD=2EC,N为PB的中点,求证: 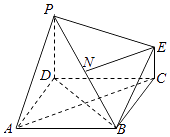
(1)平面EBC∥平面PDA;
(2)NE⊥平面PDB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥S﹣ABC中,△ABC是边长为2 ![]() 的正三角形,平面SAC⊥平面ABC,SA=SC=2,M、N分别为AB、SB的中点.
的正三角形,平面SAC⊥平面ABC,SA=SC=2,M、N分别为AB、SB的中点. 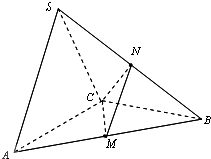
(1)证明:AC⊥SB;
(2)求三棱锥B﹣CMN的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点Pn(an , bn)满足an+1=an·bn+1 , bn+1=(n∈N*)且点P1的坐标为(1,-1).
(1)求过点P1 , P2的直线l的方程;
(2)试用数学归纳法证明:对于n∈N* , 点Pn都在(1)中的直线l上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x+2﹣x . (Ⅰ)试写出这个函数的性质(不少于3条,不必说明理由),并作出图象;
(Ⅱ)设函数g(x)=4x+4﹣x﹣af(x),求这个函数的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,其中 n 为正整数.
,其中 n 为正整数.
(1)求f(1),f(2),f(3) 的值;
(2)猜想满足不等式 f(n)<0 的正整数 n 的范围,并用数学归纳法证明你的猜想.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=|log2x|的定义域为[ ![]() ,n](m,n为正整数),值域为[0,2],则满足条件的整数对(m,n)共有( )
,n](m,n为正整数),值域为[0,2],则满足条件的整数对(m,n)共有( )
A.1个
B.7个
C.8个
D.16个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com